一、项目功能需求：将 HTML 中 span 元素集合映射成 SVG 格式文件。

　　参数： span 的绝对定位坐标和 transform 的集合，贝塞尔曲线的锚点绝对定位坐标和控制点绝对定位坐标（根据曲线路径绘制 span ），span 集合父容器的宽度和高度。

　　输出： svg 的字符串形式。

二、知识点：由于涉及到 css 的 transform 样式，所以会用 Matrix 的相关理论知识。

　　1. 沿着路径变化的文字： svg 中提供了 <textPath> 元素来产生文字沿着某条事先定义好的曲线路径排列的效果；

<svg>    <defs>        <path id="pathPreDef" d="相应路径值" />    </defs>    <text fill="#000">        <textPath xlink:href="#pathPreDef">文本内容</textPath>    </text></svg>

example

　　2. svg 坐标系统：

　　viewBox 属性用来重新定义视口的坐标范围，从而默认的坐标度量单位也会随之改变。

　　<svg width="3cm" height="3cm" viewBox="0 0 300 300">...</svg>

　　使默认的用户坐标系度量单位变为 0.01cm. (注：四个参数为 left top width height)

　　3. 三次贝塞尔曲线的绘制：

　　曲线的定义有四个点： 起始点、终止点（都称为锚点）和两个相互分离的中间点（都称为控制点）。

　　svg 中绘制命令（数据）为： "C x1 y1 x2 y2 destx desty" （x1 y1 为控制点1， x2 y2 为控制点2， destx desty 为终点， C 为普通绘制）

　　除了普通绘制，还有 S 的光滑绘制，区别在于少一个控制点，即 S 只有一个控制点。

　　4. svg 中的相关 transform 矩阵格式

　　rotate: [cos(a) sina(a) -sin(a) cos(a) 0 0]　　(a 为旋转的 rad， deg = rad / π * 180)

　　swekedX: [1 0 tan(a) 1 0 0]

　　swekedY: [1 tan(a) 0 1 0 0]

　　scale: [sx 0 0 sy 0 0]　　（sx 为依 x 轴缩放比例， sy 为依 y 轴缩放比例）

　　 = [a b c d e f]

　　（详见 W3C SVG 标准文档）

　　5. 二维坐标系的矩阵变换公式

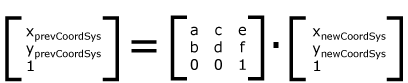
　　（参见 SVG 元素转换后的坐标，即求逆矩阵）

三、相关代码及所用类库：

　　1. 矩阵乘：（后来找到了一个类库被取代了）

function _matrixMultiply(arr1, arr2) {            var returnArr = [],                lenCol = arr1[0].length > arr2[0].length ? arr1[0].length : arr2[0].length,                lenRow = arr1.length > arr2.length ? arr1.length : arr2.length,                i, j, arr1Item, arr2Item, sum;            for (i = 0; i < lenRow; i++) {//row                sum = 0;                returnArr[i] = [];                for (j = 0; j < lenCol; j++) {//col                    returnArr[i][j] = _pointSum(i, j, arr1, arr2);                }            }            return returnArr;        }        function _pointSum(i, j, arr1, arr2, undefined) {            var sum = 0, index = 0, isArr1Spill = false, isArr2Spill = false;            while (!isArr1Spill || !isArr2Spill) {                isArr1Spill = arr1[i] === undefined || arr1[i][index] === undefined;                isArr2Spill = arr2[index] === undefined || arr2[index][j] === undefined;                sum += (isArr1Spill ? 0 : arr1[i][index]) * (isArr2Spill ? 0 : arr2[index][j]);                index++;            }            return sum;        }

　　2. Matrix 类库：sylvester

　　Matrix.create([[],[],[]]) 返回 Matrix 对象；
　　　　.elements 属性包含矩阵值
　　　　.multiply(MatrixObject) 方法求乘机
　　　　.inverse() 方法获取逆矩阵
end