主程序：

function [center, U, obj_fcn] = FCMClust(data, cluster_n, options)
    % 采用模糊C均值对数据集data聚为cluster_n类 
    % 用法：
    %   1.  [center,U,obj_fcn] = FCMClust(Data,N_cluster,options);
    %   2.  [center,U,obj_fcn] = FCMClust(Data,N_cluster);
    % 输入：
    %   data        ---- N-by-D矩阵,表示N个样本,每个样本具有D维特征
    %   N_cluster   ---- 标量K,表示聚类数目（即类别数）
    %   options     ---- 4x1矩阵，其中
    %       options(1):  隶属度矩阵U的指数，>1               (缺省值: 2.0)
    %       options(2):  最大迭代次数                         (缺省值: 100)
    %       options(3):  隶属度最小变化量,迭代终止条件    (缺省值: 1e-5)
    %       options(4):  每次迭代是否输出信息                 (缺省值: 1)
    % 输出：
    %   center      ---- 聚类中心,K-by-D
    %   U           ---- 隶属度矩阵，K-by-N
    %   obj_fcn     ---- 目标函数值，iter_n-by-1
    
    % 判断输入参数个数只能是2个或3个
    if nargin ~= 2 & nargin ~= 3    
        error(‘Too many or too few input arguments!‘);
    end
    data_n = size(data, 1); % 求出data的第一维(rows)数,即样本个数
    in_n = size(data, 2);   % 求出data的第二维(columns)数，即数据维度
    % 默认操作参数
    default_options = [ 2;              % 隶属度矩阵U的指数
                        100;            % 最大迭代次数 
                        1e-5;           % 目标函数最小变化量,迭代终止条件
                        1];             % 每次迭代是否输出信息，标志1显示 
    % 如果输入参数个数为2，那么就调用默认的option参数
    if nargin == 2
        options = default_options;
     else       % 分析有options做参数时候的情况
        % 如果用户给的opition参数少于4个,那么其他用默认值
        if length(options) < 4
            tmp = default_options;
            tmp(1:length(options)) = options;
            options = tmp;
        end
        % 返回options中值为NaN的索引位置
        nan_index = find(isnan(options)==1);
        % 将denfault_options中对应位置的参数值赋给options中值为NaN的值
        options(nan_index) = default_options(nan_index);
        if options(1) <= 1  %如果模糊矩阵的指数小于等于1
            error(‘The exponent should be greater than 1!‘);
        end
    end
    %将options 中的分量分别赋值给四个变量;
    expo = options(1);          % 隶属度矩阵U的指数
    max_iter = options(2);% 最大迭代次数 
    min_impro = options(3);% 目标函数最小变化量,迭代终止条件
    display = options(4);% 每次迭代是否输出信息 
    % 初始化目标函数obj_fcn
    obj_fcn = zeros(max_iter, 1);
    % 初始化隶属度矩阵,使U满足列上相加为1
    U = initfcm(cluster_n, data_n);     
    % 主要循环
    for i = 1:max_iter
        % 在第i步循环中改变聚类中心ceneter和隶属度U的值;
        [U, center, obj_fcn(i)] = stepfcm(data, U, cluster_n, expo);
        if display 
            fprintf(‘FCM:Iteration count = %d, obj.fcn = %f\n‘, i, obj_fcn(i));
        end
        % 终止条件判别
        if i > 1
            if abs(obj_fcn(i) - obj_fcn(i-1)) < min_impro
                break; 
            end
        end
    end
    % 实际迭代次数 
    iter_n = i;
    % 清除迭代次数之后的值
    obj_fcn(iter_n+1:max_iter) = [];  
end
% 初始化fcm的隶属度函数矩阵，满足列向量之和为1
function U = initfcm(cluster_n, data_n)
    % 输入:
    %   cluster_n   ---- 聚类中心个数
    %   data_n      ---- 样本点数
    % 输出：
    %   U           ---- 初始化的隶属度矩阵
    U = rand(cluster_n, data_n);
    col_sum = sum(U);
    U = U./col_sum(ones(cluster_n, 1), :);
end
% 模糊C均值聚类时迭代的一步
function [U_new, center, obj_fcn] = stepfcm(data, U, cluster_n, expo)
    % 输入：
    %   data        ---- 训练样本,表示N个样本,每个样本具有D维特征，N-by-D
    %   U           ---- 隶属度矩阵，K-by-N
    %   cluster_n   ---- 聚合数目(类别数),K
    %   expo        ---- 隶属度矩阵U的指数                      
    % 输出：
    %   U_new       ---- 迭代计算出的新的隶属度矩阵,K-by-N
    %   center      ---- 迭代计算出的新的聚类中心,K-by-D
    %   obj_fcn     ---- 目标函数值
    % 隶属度矩阵进行指数运算结果，K-by-N
    mf = U.^expo; 
    % 计算新聚类中心,K-by-D
    center = mf*data./(sum(mf,2)*ones(1,size(data,2))); 
    % 计算距离矩阵,K-by-N
    distMat = dist(center,data‘);      
    % 计算目标函数值
    obj_fcn = sum(sum((distMat.^2).*mf));  
    tmp = distMat.^(-2/(expo-1));      
    % 计算新的隶属度矩阵
    U_new = tmp./(ones(cluster_n, 1)*sum(tmp));
end

测试：

clc
clear
close all
data = importdata(‘data/seed.txt‘);
K=3;
%% 模型训练阶段
options = [2 10000 NaN 0];
% [center,U,obj_fcn] = fcm(data(:,1:7),K,options);
[center,U,obj_fcn] = FCMClust(data(:,1:7),K,options);
% [center,U,obj_fcn] = KFCMClust(data(:,1:7),K,10,options);
%% 准确率评估
[~,label] = max(U); %找到所属的类
subplot(1,2,1);
gscatter(data(:,4),data(:,7),data(:,8)),title(‘choose:4,7列,理论结果‘)
% cal accuracy
a_1 = size(find(label(1:70)==1),2);
a_2 = size(find(label(1:70)==2),2);
a_3 = size(find(label(1:70)==3),2);
a = max([a_1,a_2,a_3]);
b_1 = size(find(label(71:140)==1),2);
b_2 = size(find(label(71:140)==2),2);
b_3 = size(find(label(71:140)==3),2);
b = max([b_1,b_2,b_3]);
c_1 = size(find(label(141:210)==1),2);
c_2 = size(find(label(141:210)==2),2);
c_3 = size(find(label(141:210)==3),2);
c = max([c_1,c_2,c_3]);
accuracy = (a+b+c)/210
% plot answer
subplot(1,2,2);
gscatter(data(:,4),data(:,7),label),title([‘实际结果,accuracy=‘,num2str(accuracy)])

输出结果：

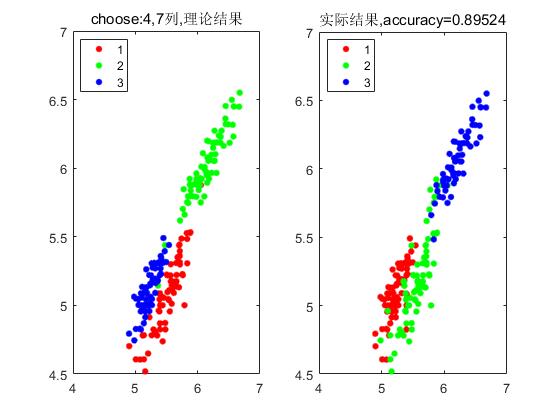
附录seed数据集：

15.26 14.84 0.871 5.763 3.312 2.221 5.22 1

14.88 14.57 0.8811 5.554 3.333 1.018 4.956 1

14.29 14.09 0.905 5.291 3.337 2.699 4.825 1

13.84 13.94 0.8955 5.324 3.379 2.259 4.805 1

16.14 14.99 0.9034 5.658 3.562 1.355 5.175 1

14.38 14.21 0.8951 5.386 3.312 2.462 4.956 1

14.69 14.49 0.8799 5.563 3.259 3.586 5.219 1

14.11 14.1 0.8911 5.42 3.302 2.7     5       1

16.63 15.46 0.8747 6.053 3.465 2.04 5.877 1

16.44 15.25 0.888 5.884 3.505 1.969 5.533 1

15.26 14.85 0.8696 5.714 3.242 4.543 5.314 1

14.03 14.16 0.8796 5.438 3.201 1.717 5.001 1

13.89 14.02 0.888 5.439 3.199 3.986 4.738 1

13.78 14.06 0.8759 5.479 3.156 3.136 4.872 1

13.74 14.05 0.8744 5.482 3.114 2.932 4.825 1

14.59 14.28 0.8993 5.351 3.333 4.185 4.781 1

13.99 13.83 0.9183 5.119 3.383 5.234 4.781 1

15.69 14.75 0.9058 5.527 3.514 1.599 5.046 1

14.7 14.21 0.9153 5.205 3.466 1.767 4.649 1

12.72 13.57 0.8686 5.226 3.049 4.102 4.914 1

14.16 14.4 0.8584 5.658 3.129 3.072 5.176 1

14.11 14.26 0.8722 5.52 3.168 2.688 5.219 1

15.88 14.9 0.8988 5.618 3.507 0.7651 5.091 1

12.08 13.23 0.8664 5.099 2.936 1.415 4.961 1

15.01 14.76 0.8657 5.789 3.245 1.791 5.001 1

16.19 15.16 0.8849 5.833 3.421 0.903 5.307 1

13.02 13.76 0.8641 5.395 3.026 3.373 4.825 1

12.74 13.67 0.8564 5.395 2.956 2.504 4.869 1

14.11 14.18 0.882 5.541 3.221 2.754 5.038 1

13.45 14.02 0.8604 5.516 3.065 3.531 5.097 1

13.16 13.82 0.8662 5.454 2.975 0.8551 5.056 1

15.49 14.94 0.8724 5.757 3.371 3.412 5.228 1

14.09 14.41 0.8529 5.717 3.186 3.92 5.299 1

13.94 14.17 0.8728 5.585 3.15 2.124 5.012 1

15.05 14.68 0.8779 5.712 3.328 2.129 5.36 1

16.12 15      0.9     5.709 3.485 2.27 5.443 1

16.2 15.27 0.8734 5.826 3.464 2.823 5.527 1

17.08 15.38 0.9079 5.832 3.683 2.956 5.484 1

14.8 14.52 0.8823 5.656 3.288 3.112 5.309 1

14.28 14.17 0.8944 5.397 3.298 6.685 5.001 1

13.54 13.85 0.8871 5.348 3.156 2.587 5.178 1

13.5 13.85 0.8852 5.351 3.158 2.249 5.176 1

13.16 13.55 0.9009 5.138 3.201 2.461 4.783 1

15.5 14.86 0.882 5.877 3.396 4.711 5.528 1

15.11 14.54 0.8986 5.579 3.462 3.128 5.18 1

13.8 14.04 0.8794 5.376 3.155 1.56 4.961 1

15.36 14.76 0.8861 5.701 3.393 1.367 5.132 1

14.99 14.56 0.8883 5.57 3.377 2.958 5.175 1

14.79 14.52 0.8819 5.545 3.291 2.704 5.111 1

14.86 14.67 0.8676 5.678 3.258 2.129 5.351 1

14.43 14.4 0.8751 5.585 3.272 3.975 5.144 1

15.78 14.91 0.8923 5.674 3.434 5.593 5.136 1

14.49 14.61 0.8538 5.715 3.113 4.116 5.396 1

14.33 14.28 0.8831 5.504 3.199 3.328 5.224 1

14.52 14.6 0.8557 5.741 3.113 1.481 5.487 1

15.03 14.77 0.8658 5.702 3.212 1.933 5.439 1

14.46 14.35 0.8818 5.388 3.377 2.802 5.044 1

14.92 14.43 0.9006 5.384 3.412 1.142 5.088 1

15.38 14.77 0.8857 5.662 3.419 1.999 5.222 1

12.11 13.47 0.8392 5.159 3.032 1.502 4.519 1

11.42 12.86 0.8683 5.008 2.85 2.7     4.607 1

11.23 12.63 0.884 4.902 2.879 2.269 4.703 1

12.36 13.19 0.8923 5.076 3.042 3.22 4.605 1

13.22 13.84 0.868 5.395 3.07 4.157 5.088 1

12.78 13.57 0.8716 5.262 3.026 1.176 4.782 1

12.88 13.5 0.8879 5.139 3.119 2.352 4.607 1

14.34 14.37 0.8726 5.63 3.19 1.313 5.15 1

14.01 14.29 0.8625 5.609 3.158 2.217 5.132 1

14.37 14.39 0.8726 5.569 3.153 1.464 5.3     1

12.73 13.75 0.8458 5.412 2.882 3.533 5.067 1

17.63 15.98 0.8673 6.191 3.561 4.076 6.06 2

16.84 15.67 0.8623 5.998 3.484 4.675 5.877 2

17.26 15.73 0.8763 5.978 3.594 4.539 5.791 2

19.11 16.26 0.9081 6.154 3.93 2.936 6.079 2

16.82 15.51 0.8786 6.017 3.486 4.004 5.841 2

16.77 15.62 0.8638 5.927 3.438 4.92 5.795 2

17.32 15.91 0.8599 6.064 3.403 3.824 5.922 2

20.71 17.23 0.8763 6.579 3.814 4.451 6.451 2

18.94 16.49 0.875 6.445 3.639 5.064 6.362 2

17.12 15.55 0.8892 5.85 3.566 2.858 5.746 2

16.53 15.34 0.8823 5.875 3.467 5.532 5.88 2

18.72 16.19 0.8977 6.006 3.857 5.324 5.879 2

20.2 16.89 0.8894 6.285 3.864 5.173 6.187 2

19.57 16.74 0.8779 6.384 3.772 1.472 6.273 2

19.51 16.71 0.878 6.366 3.801 2.962 6.185 2

18.27 16.09 0.887 6.173 3.651 2.443 6.197 2

18.88 16.26 0.8969 6.084 3.764 1.649 6.109 2

18.98 16.66 0.859 6.549 3.67 3.691 6.498 2

21.18 17.21 0.8989 6.573 4.033 5.78 6.231 2

20.88 17.05 0.9031 6.45 4.032 5.016 6.321 2

20.1 16.99 0.8746 6.581 3.785 1.955 6.449 2

18.76 16.2 0.8984 6.172 3.796 3.12 6.053 2

18.81 16.29 0.8906 6.272 3.693 3.237 6.053 2

18.59 16.05 0.9066 6.037 3.86 6.001 5.877 2

18.36 16.52 0.8452 6.666 3.485 4.933 6.448 2

16.87 15.65 0.8648 6.139 3.463 3.696 5.967 2

19.31 16.59 0.8815 6.341 3.81 3.477 6.238 2

18.98 16.57 0.8687 6.449 3.552 2.144 6.453 2

18.17 16.26 0.8637 6.271 3.512 2.853 6.273 2

18.72 16.34 0.881 6.219 3.684 2.188 6.097 2

16.41 15.25 0.8866 5.718 3.525 4.217 5.618 2

17.99 15.86 0.8992 5.89 3.694 2.068 5.837 2

19.46 16.5 0.8985 6.113 3.892 4.308 6.009 2

19.18 16.63 0.8717 6.369 3.681 3.357 6.229 2

18.95 16.42 0.8829 6.248 3.755 3.368 6.148 2

18.83 16.29 0.8917 6.037 3.786 2.553 5.879 2

18.85 16.17 0.9056 6.152 3.806 2.843 6.2 2

17.63 15.86 0.88 6.033 3.573 3.747 5.929 2

19.94 16.92 0.8752 6.675 3.763 3.252 6.55 2

18.55 16.22 0.8865 6.153 3.674 1.738 5.894 2

18.45 16.12 0.8921 6.107 3.769 2.235 5.794 2

19.38 16.72 0.8716 6.303 3.791 3.678 5.965 2

19.13 16.31 0.9035 6.183 3.902 2.109 5.924 2

19.14 16.61 0.8722 6.259 3.737 6.682 6.053 2

20.97 17.25 0.8859 6.563 3.991 4.677 6.316 2

19.06 16.45 0.8854 6.416 3.719 2.248 6.163 2

18.96 16.2 0.9077 6.051 3.897 4.334 5.75 2

19.15 16.45 0.889 6.245 3.815 3.084 6.185 2

18.89 16.23 0.9008 6.227 3.769 3.639 5.966 2

20.03 16.9 0.8811 6.493 3.857 3.063 6.32 2

20.24 16.91 0.8897 6.315 3.962 5.901 6.188 2

18.14 16.12 0.8772 6.059 3.563 3.619 6.011 2

16.17 15.38 0.8588 5.762 3.387 4.286 5.703 2

18.43 15.97 0.9077 5.98 3.771 2.984 5.905 2

15.99 14.89 0.9064 5.363 3.582 3.336 5.144 2

18.75 16.18 0.8999 6.111 3.869 4.188 5.992 2

18.65 16.41 0.8698 6.285 3.594 4.391 6.102 2

17.98 15.85 0.8993 5.979 3.687 2.257 5.919 2

20.16 17.03 0.8735 6.513 3.773 1.91 6.185 2

17.55 15.66 0.8991 5.791 3.69 5.366 5.661 2

18.3 15.89 0.9108 5.979 3.755 2.837 5.962 2

18.94 16.32 0.8942 6.144 3.825 2.908 5.949 2

15.38 14.9 0.8706 5.884 3.268 4.462 5.795 2

16.16 15.33 0.8644 5.845 3.395 4.266 5.795 2

15.56 14.89 0.8823 5.776 3.408 4.972 5.847 2

15.38 14.66 0.899 5.477 3.465 3.6     5.439 2

17.36 15.76 0.8785 6.145 3.574 3.526 5.971 2

15.57 15.15 0.8527 5.92 3.231 2.64 5.879 2

15.6 15.11 0.858 5.832 3.286 2.725 5.752 2

16.23 15.18 0.885 5.872 3.472 3.769 5.922 2

13.07 13.92 0.848 5.472 2.994 5.304 5.395 3

13.32 13.94 0.8613 5.541 3.073 7.035 5.44 3

13.34 13.95 0.862 5.389 3.074 5.995 5.307 3

12.22 13.32 0.8652 5.224 2.967 5.469 5.221 3

11.82 13.4 0.8274 5.314 2.777 4.471 5.178 3

11.21 13.13 0.8167 5.279 2.687 6.169 5.275 3

11.43 13.13 0.8335 5.176 2.719 2.221 5.132 3

12.49 13.46 0.8658 5.267 2.967 4.421 5.002 3

12.7 13.71 0.8491 5.386 2.911 3.26 5.316 3

10.79 12.93 0.8107 5.317 2.648 5.462 5.194 3

11.83 13.23 0.8496 5.263 2.84 5.195 5.307 3

12.01 13.52 0.8249 5.405 2.776 6.992 5.27 3

12.26 13.6 0.8333 5.408 2.833 4.756 5.36 3

11.18 13.04 0.8266 5.22 2.693 3.332 5.001 3

11.36 13.05 0.8382 5.175 2.755 4.048 5.263 3

11.19 13.05 0.8253 5.25 2.675 5.813 5.219 3

11.34 12.87 0.8596 5.053 2.849 3.347 5.003 3

12.13 13.73 0.8081 5.394 2.745 4.825 5.22 3

11.75 13.52 0.8082 5.444 2.678 4.378 5.31 3

11.49 13.22 0.8263 5.304 2.695 5.388 5.31 3

12.54 13.67 0.8425 5.451 2.879 3.082 5.491 3

12.02 13.33 0.8503 5.35 2.81 4.271 5.308 3

12.05 13.41 0.8416 5.267 2.847 4.988 5.046 3

12.55 13.57 0.8558 5.333 2.968 4.419 5.176 3

11.14 12.79 0.8558 5.011 2.794 6.388 5.049 3

12.1 13.15 0.8793 5.105 2.941 2.201 5.056 3

12.44 13.59 0.8462 5.319 2.897 4.924 5.27 3

12.15 13.45 0.8443 5.417 2.837 3.638 5.338 3

11.35 13.12 0.8291 5.176 2.668 4.337 5.132 3

11.24 13      0.8359 5.09 2.715 3.521 5.088 3

11.02 13      0.8189 5.325 2.701 6.735 5.163 3

11.55 13.1 0.8455 5.167 2.845 6.715 4.956 3

11.27 12.97 0.8419 5.088 2.763 4.309 5       3

11.4 13.08 0.8375 5.136 2.763 5.588 5.089 3

10.83 12.96 0.8099 5.278 2.641 5.182 5.185 3

10.8 12.57 0.859 4.981 2.821 4.773 5.063 3

11.26 13.01 0.8355 5.186 2.71 5.335 5.092 3

10.74 12.73 0.8329 5.145 2.642 4.702 4.963 3

11.48 13.05 0.8473 5.18 2.758 5.876 5.002 3

12.21 13.47 0.8453 5.357 2.893 1.661 5.178 3

11.41 12.95 0.856 5.09 2.775 4.957 4.825 3

12.46 13.41 0.8706 5.236 3.017 4.987 5.147 3

12.19 13.36 0.8579 5.24 2.909 4.857 5.158 3

11.65 13.07 0.8575 5.108 2.85 5.209 5.135 3

12.89 13.77 0.8541 5.495 3.026 6.185 5.316 3

11.56 13.31 0.8198 5.363 2.683 4.062 5.182 3

11.81 13.45 0.8198 5.413 2.716 4.898 5.352 3

10.91 12.8 0.8372 5.088 2.675 4.179 4.956 3

11.23 12.82 0.8594 5.089 2.821 7.524 4.957 3

10.59 12.41 0.8648 4.899 2.787 4.975 4.794 3

10.93 12.8 0.839 5.046 2.717 5.398 5.045 3

11.27 12.86 0.8563 5.091 2.804 3.985 5.001 3

11.87 13.02 0.8795 5.132 2.953 3.597 5.132 3

10.82 12.83 0.8256 5.18 2.63 4.853 5.089 3

12.11 13.27 0.8639 5.236 2.975 4.132 5.012 3

12.8 13.47 0.886 5.16 3.126 4.873 4.914 3

12.79 13.53 0.8786 5.224 3.054 5.483 4.958 3

13.37 13.78 0.8849 5.32 3.128 4.67 5.091 3

12.62 13.67 0.8481 5.41 2.911 3.306 5.231 3

12.76 13.38 0.8964 5.073 3.155 2.828 4.83 3

12.38 13.44 0.8609 5.219 2.989 5.472 5.045 3

12.67 13.32 0.8977 4.984 3.135 2.3     4.745 3

11.18 12.72 0.868 5.009 2.81 4.051 4.828 3

12.7 13.41 0.8874 5.183 3.091 8.456 5       3

12.37 13.47 0.8567 5.204 2.96 3.919 5.001 3

12.19 13.2 0.8783 5.137 2.981 3.631 4.87 3

11.23 12.88 0.8511 5.14 2.795 4.325 5.003 3

13.2 13.66 0.8883 5.236 3.232 8.315 5.056 3

11.84 13.21 0.8521 5.175 2.836 3.598 5.044 3

12.3 13.34 0.8684 5.243 2.974 5.637 5.063 3

本文出自 “IT技术学习与交流” 博客，谢绝转载！

FCM详解