一、基本原理：

    假设我们使用一个下标范围比较大的数组来存储元素。设计一个函数（哈希函数，也叫做散列函数），使得每个元素的关键字经过函数运算得到一个函数值（即数组下标），于是用这个数组单元来存储这个元素。通过函数值即数组下标就可以查找数据元素了。

    直接定址”与“解决冲突”是哈希表的两大特点。

二、优点：

    把数据的存储和查找消耗的时间大大降低，几乎可以看成是常数时间；而代价仅仅是消耗比较多的内存。然而在当前可利用内存越来越多的情况下，用空间换时间的做法是值得的。

三、构造方法：

尽力避免冲突但函数也需要易于编码，即易于实现。

１、直接定址法

    例：有一个从1到100岁的人口数字统计表，其中，年龄作为关键字，哈希函数取关键字自身。但这种方法效率不高,时间复杂度是O(1),空间复杂度是O(n),n是关键字的个数

２、数字分析法

３、平方取中法

    取关键字平方后的中间几位为哈希地址。

４、折叠法

    将关键字分割成位数相同的几部分（最后一部分的位数可以不同），然后取这几部分的叠加和（舍去进位）作为哈希地址，这方法称为折叠法。

这种方法适用于关键字位数较多，而且关键字中每一位上数字分布大致均匀的情况。 

    折叠法中数位折叠又分为移位叠加和边界叠加两种方法，移位叠加是将分割后是每一部分的最低位对齐，然后相加；边界叠加是从一端向另一端沿分割界来回折叠，然后对齐相加。 

例：当哈希表长为1000时，关键字key=110108331119891，允许的地址空间为三位十进制数，则这两种叠加情况如下

       移位叠加891+119+331+108+110=(1)559

       边界叠加  891+911+331+801+110=(3)044

    用移位叠加得到的哈希地址是559，而用边界叠加所得到的哈希地址是44。如果关键字不是数值而是字符串，则可先转化为数。转化的办法可以用ASCⅡ字符或字符的次序值。

５、除留余数法

    取关键字被某个不大于哈希表表长m的数p除后所得余数为哈希地址。H(key)=key MOD p (p<=m)

６、随机数法

    选择一个随机函数，取关键字的随机函数值为它的哈希地址，即H(key)=random(key) ,其中random为随机函数。通常用于关键字长度不等时采用此法。

四、冲突问题：

1.问题冲突：可能经过同一哈希函数的计算，把不同的关键字映射到了同一个地址上面。

2.解决冲突：

（1）“桶”算法：

    假设哈希表有m 个地址，就将其改为 m 个“桶”，其桶号与哈希地址一一对应，每个桶都用来存放互为同义词的键，也就是如果两个不同的键用哈希函数计算得到了同一个哈希地址，就将它们放到同一个桶中，检索的时候在桶内进行顺序检索。

（2）开放定址法

    开放定址法又分为线性探插法、二次探查法和双重散列法等。开放定址法解决冲突的基本思想是：使用某种方法在散列表中形成一个探查序列，沿着次序列逐个单元进行查找，直到找到一个空闲的单元时将新结点存入其中。假设散列表空间为T[0..m-1]，散列函数H(key)，开放定址法的一般形式为：hi=(H(key)+di)% m 0≤i≤m-1 其中di为增量序列，m为散列表长。h0=H(key)为初始探查地址(假d0=0),后续的探查地址依次是h1,h2,…,hm-1 。

    ①线性探查法

    该方法的基本思想是：将散列表T[0..m-1]看成是一个循环向量，若初始探查的地址为d(即h(key)=d)，则最长的探查序列为：d，d+l，d+2，…，m-1，0，1，…，d-1即:探查时从地址d开始，首先探查T[d]，然后依次探查T[d+1]，…，直到T[m-1]，此后又循环到T[0]，T[1]，…，直到探查到T[d-1]为止。线性探查法的探查序列为：hi=(h(key)+i)％m 0≤i≤m-1

    优点：用线性探测法处理冲突，思路清晰，算法简单。

    缺点：

    处理溢出需另编程序。一般可另外设立一个溢出表，专门用来存放上述哈希表中放不下的记录。此溢出表最简单的结构是顺序表，查找方法可用顺序查找。

    删除工作非常困难。假如要从哈希表 HT 中删除一个记录，不能将这个记录所在位置置为空，而只能标上已被删除的标记，否则，将会影响以后的查找。

    线性探测法很容易产生堆聚现象。所谓堆聚现象，就是存入哈希表的记录在表中连成一片。按照线性探测法处理冲突，如果生成哈希地址的连续序列愈长 ( 即不同关键字值的哈希地址相邻在一起愈长 ) ，则当新的记录加入该表时，与这个序列发生冲突的可能性愈大。因此，哈希地址的较长连续序列比较短连续序列生长得快，这就意味着，一旦出现堆聚 ( 伴随着冲突 ) ，就将引起进一步的堆聚。

    ② 线性补偿探测法 
    线性补偿探测法的基本思想是：
将线性探测的步长从 1 改为 Q ，即将上述算法中的 j ＝ (j＋ 1) % m 改为： j ＝ (j＋ Q) % m ，而且要求 Q 与 m 是互质的，以便能探测到哈希表中的所有单元。

    ③随机探测法：
    将线性探测的步长从常数改为随机数，即令： j ＝ (j ＋ RN) % m ，其中 RN是一个随机数。在实际程序中应预先用随机数发生器产生一个随机序列，将此序列作为依次探测的步长。这样就能使不同的关键字具有不同的探测次序，从而可以避免或减少堆聚。基于与线性探测法相同的理由，在线性补偿探测法和随机探测法中，删除一个记录后也要打上删除标记。

    ④二次探查法

　　二次探查法的探查序列是:hi=(H(key)+i2) % m 0≤i≤m-1

即探查序列为：d=H(key),d+12,d+22,…,等。也就是说，探查从地址d开始，先探查T[d],然后在依次探查T[d+12],T[d+22],…。

    ⑤  双重散列法

　　双重散列法是几种方法中最好的方法，它的探查序列为：hi=(H(key)+i*H1(key)) % m 0≤i≤m-1

即探查序列为：d=H(key),(d+1*H1(key))% m，(d+2*H1(key)) % m，…，等。

（3）拉链法（链地址法）

当存储结构是链表时，多采用拉链法，用拉链法处理冲突的办法是：把具有相同散列地址的关键字(同义词)值放在同一个单链表中，称为同义词链表。有m个散列地址就有m个链表，同时用指针数组T[0..m-1]存放各个链表的头指针，凡是散列地址为i的记录都以结点方式插入到以T[i]为指针的单链表中。T中各分量的初值应为空指针。

    与开放定址法相比，拉链法有如下几个优点：
        ①拉链法处理冲突简单，且无堆积现象，即非同义词决不会发生冲突，因此平均查找长度较短；
        ②由于拉链法中各链表上的结点空间是动态申请的，故它更适合于造表前无法确定表长的情况；
        ③开放定址法为减少冲突，要求装填因子α较小，故当结点规模较大时会浪费很多空间。而拉链法中可取α≥1，且结点较大时，拉链法中增加的指针域可忽略不计，因此节省空间；
        ④在用拉链法构造的散列表中，删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。而对开放地址法构造的散列表，删除结点不能简单地将被删结点的空间置为空，否则将截断在它之后填人散列表的同义词结点的查找路径。这是因为各种开放地址法中，空地址单元(即开放地址)都是查找失败的条件。因此在用开放地址法处理冲突的散列表上执行删除操作，只能在被删结点上做删除标记，而不能真正删除结点。

理解线性探测法和拉链法例题：

设散列函数为h(key)=key % 11；散列地址表空间为0~10，对关键字序列{27，13，55，32，18，49，24，38，43}，利用线性探测法解决冲突，构造散列表。

　　解：首先根据散列函数计算散列地址：

　　　　h(27)=5； h(13)=2；

　　　　h(55)=0； h(32)=10；

　　　　h(18)=7； h(49)=5；

　　　　h(24)=2； h(38)=5；

　　　　h(43)=10；　

　　(散列表各元素查找比较次数标注在结点的上方或下方)

根据散列函数计算得到的散列地址可知，关键字27、13、55、32、18插入的地址均为开放地址，将它们直接插入到T[5],T[2],T[0],T[10],T[7]中。当插入关键字49时，散列地址5已被同义词27占用，因此探查h1=(5+1)% 11=6，此地址为开放地址，因此可将49插入到T[6]中；当插入关键字24时，其散列地址2已被同义词13占用，故探测地址h1=(2+1) % 11=3, 此地址为开放地址，因此可将24插入到T[3]中；当关键字38插入时，散列地址5已被同义词27占用，探查h1=(5+1) % 11=6,也被同义词49占用，再探查h2=(5+2)%11=7，地址7已被非同义词占用，因此需要再探查h3=(5+3) % 11=8，此地址为开放地址，因此可将38插入到T[8]中；当插入关键字43时，计算得到散列地址10已被关键字32占用，需要探查h1=(10+1)% 11=0,此地址已被占用，探查h2=(10+1) % 11=1为开放地址，因此可将43插入到T[1]中；

对用线性探测法构造的散列表的平均查找长度为：

　　　　ASL=(1×5＋2×2＋3×1＋4×1)/9 ≈1.78

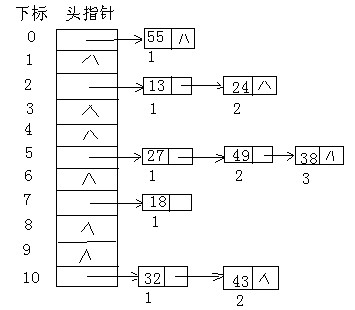
而用拉链法构造的散列表上查找成功的平均查找长度为：

　　　　ASL=(1×5+2×3+3×1)/9≈1.55

显然，开放定址法处理冲突的的平均查找长度要高于拉链法处理冲突的平均查找长度。但它们都比前面介绍的其它查找方法的平均查找长度要短。

本文出自 “java我的最爱” 博客，请务必保留此出处http://lindianli.blog.51cto.com/7129432/1547923

哈希表知识点总结