转自：http://blog.csdn.net/xianlingmao/article/details/7768833

引入

我们会遇到很多问题无法用分析的方法来求得精确解，例如由于式子特别，真的解不出来。这时就需要找一种方法求其近似解，并且有手段能测量出这种解的近似程度 （比如渐进性，上下限什么的）

随机模拟的基本思想

现在假设我们有一个矩形的区域R（大小已知），在这个区域中有一个不规则的区域M（即不能通过公式直接计算出来），现在要求取M的面积？ 怎么求？近似的方法很多，例如：把这个不规则的区域M划分为很多很多个小的规则区域，用这些规则区域的面积求和来近似M，另外一个近似的方法就是采样的方法，我们抓一把黄豆，把它们均匀地铺在矩形区域，如果我们知道黄豆的总个数S，那么只要我们数数位于不规则区域M中的黄豆个数S1，那么我们就可以求出M的面积：M=S1*R/S。

 

在机器学习或统计计算领域，我们常常遇到这样一类问题：即如何求取一个定积分：\inf _a ^b f(x) dx， 如归一化因子等。

如何来求解这类问题呢？当然如果定积分可以解析求出，直接求出即可，如果不能解析求出，只能求取近似解了，常用的近似方法是采用蒙特卡洛积分，即把上述式子改写为：

\inf _a^b f(x)*g(x)/g(x) dx = \inf _a^b (1/g(x)) *f(x)*g(x) dx

那么把f(x)/g(x)作为一个函数，而把g(x)看做是[a,b]上的一个概率分布，抽取n个样本之后，上述式子可以继续写为：{\sum _1^n [f(x_i)/g(x_i)]}/n，当n趋向无穷大的时候，根据大数定理，上述式子是和要求的定积分式子是相等的，因此可以用抽样的方法来得到近似解。

通过上述两个例子，我们大概能够理解抽样方法解决问题的基本思想，其基本思路就是要把待解决的问题转化为一种可以通过某种采样方法可以解决的问题，至于怎么转化，还是挺有创造性，没有定法。因此随机模拟方法的核心就是如何对一个概率分布得到样本，即抽样（sampling）。

常见的抽样方法

直接抽样法

因为较为简单，而且只能解决很简单的问题，一般是一维分布的问题

 

接受-拒绝抽样（Acceptance-Rejection sampling)

为了得到一个分布的样本，我们通过某种机制得到了很多的初步样本，然后其中一部分初步样本会被作为有效的样本（即要抽取的分布的样本），一部分初步样本会被认为是无效样本舍弃掉。这个算法的基本思想是：我们需要对一个分布f(x)进行采样，但是却很难直接进行采样，所以我们想通过另外一个容易采样的分布g(x)的样本，用某种机制去除掉一些样本，从而使得剩下的样本就是来自与所求分布f(x)的样本。

它有几个条件：1）对于任何一个x，有f(x)<=M*g(x); 2) g(x)容易采样；3) g(x)最好在形状上比较接近f(x)。具体的采样过程如下：

1. 对于g(x)进行采样得到一个样本xi, xi ~ g(x);

2. 对于均匀分布采样 ui ~ U(a,b);

3. 如果ui<= f(x)/[M*g(x)], 那么认为xi是有效的样本；否则舍弃该样本； （# 这个步骤充分体现了这个方法的名字：接受-拒绝）

4. 反复重复步骤1~3，直到所需样本达到要求为止。

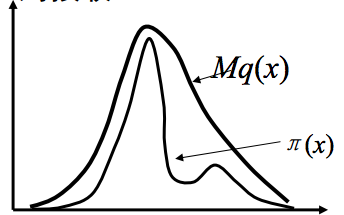
这个方法可以如图所示：

(说明：这是从其他地方弄来的图，不是自己画的，符号有些和文中不一致，其中\pi(x) 就是文中的f(x)，q(x)就是文中的g(x)  )

重要性抽样(Importance sampling)

重要性采样和蒙特卡洛积分密切相关，看积分：

\inf f(x) dx = \inf f(x)*(1/g(x))*g(x) dx, 如果g(x)是一个概率分布，从g(x)中抽取N个样本，上述的式子就约等于(1/N)* \sum f(xi)*(1/g(xi))。这相当于给每个样本赋予了一个权重，g(xi)大意味着概率大，那么N里面含有这样的样本xi就多，即这些样本的权重大，所以称为重要性抽样。

抽样的步骤如下：

1. 选择一个容易抽样的分布g(x), 从g(x)中抽取N个样本；
2. 计算(1/N)* \sum f(xi)*(1/g(xi))，从而得到近似解。

（pku，sewm，shinning）

 

MCMC抽样方法

无论是拒绝抽样还是重要性采样，都是属于独立采样，即样本与样本之间是独立无关的，这样的采样效率比较低，如拒绝采样，所抽取的样本中有很大部分是无效的，这样效率就比较低，MCMC方法是关联采样，即下一个样本与这个样本有关系，从而使得采样效率高。MCMC方法的基本思想是：通过构建一个markov chain使得该markov chain的稳定分布是我们所要采样的分布f(x)。如果这个markov chain达到稳定状态，那么来自这个chain的每个样本都是f(x)的样本，从而实现抽样的目的。

Metropolis-Hasting算法

假设要采样的概率分布是\pi(x)，现在假设有一个概率分布p(y|x)，使得\pi(x)*p(y|x) = \pi(y)*p(x|y)成立，称细致平衡公式，这个细致平衡公式是markov chain能达到稳定分布的必要条件。因此关键是构建出一个概率分布p(y|x)使得它满足细致平衡。现在假设我们有一个容易采样的分布q(y|x)（称为建议分布)，对于目前的样本x，它能够通过q(y|x)得到下一个建议样本y，这个建议样本y按照一定的概率被接受或者不被接受，称为比率\alpha(x, y) = min{1, q(x|y)*\pi(y)/[q(y|x)*\pi(x)]}。即如果知道样本xi，如何知道下一个样本x_{i+1}是什么呢？就是通过q(y|xi)得到一个建议样本y，然后根据\alpha(xi, y)决定x_{i+1}=y 还是x_{i+1}=xi。可以证明分布q(y|x)*\alpha(x,y)满足细致平衡，同时可以证明这样抽取得到的样本是分布\pi(x)的样本。具体的步骤如下：

1. 给定一个起始样本x_0和一个建议分布q(y|x)；

2. 对于第i个样本xi，通过q(y|xi)得到一个建议样本y；计算比率\alpha(xi, y)= min{1, q(xi|y)*\pi(y)/[q(y|xi)*\pi(xi)]};

3. 抽取一个均匀分布样本ui ~ U(0,1)，如果ui <= \alpha(xi,y)，则x_{i+1} = y；否则x_{i+1} = xi；

4. 重复步骤2~3，直到抽取到想要的样本数量为止。

如果，建议分布q(y|x) 满足：q(y|x) = q(x|y)，即对称，这个时候比率\alpha(x, y) = min{1, \pi(y)/\pi(x)}就是1953年最原始的算法，后来hasting把这个算法扩展了，不要求建议分布式对称的，从而得到了上述的算法。然而这个算法有一个缺点，就是抽样的效率不高，有些样本会被舍弃掉。从而产生了Gibbs算法。

Gibbs采样算法

Gibbs算法，很简单，就是用条件分布的抽样来替代全概率分布的抽样。例如，X={x1,x2,...xn}满足分布p(X)，如何对p(X)进行抽样呢？如果我们知道它的条件分布p(x1|X_{-1}),...,p(xi|X_{-i}),....，其中X_{-i}表示除了xi之外X的所有变量。如果这些条件分布都是很容易抽样的，那么我们就可以通过对条件分布的抽样来对全概率分布p(X)进行抽样。

Gibbs采样算法的步骤：

1. 给定一个初始样本X0={x10,x20,...,xn0}

2.已知一个样本Xi={x1i,x2i,...,xni}，对于x1_{i+1}进行抽样，x1_{i+1} ~ p(x1|Xi_{-1})

3. 对于x2_{i+1}进行抽样，x2_{i+1} ~ p(x2|x1_{i+1}, x3i,...xni)

................................................................

4.对于xn_{i+1}进行抽样，xn_{i+1} ~ p(xn|x1_{i+1}, x2_{i+1},...x_{n-1}_{i+1})

5.步骤2~4可以得到X的一个样本，然后重复步骤2~4可以不断地得到X的样本。

当然无论是metropolis-hasting算法还是gibbs算法，都有一个burn in的过程，所谓burn in的过程就是因为这个两个算法本身都是markov chain的算法，要达到稳定状态需要一定的步骤才能达到，所以需要一个burn in过程，只有在达到平衡状态时候得到的样本才能是平衡状态时候的目标分布的样本，因此，在burn in过程中产生的样本都需要被舍弃。如何判断一个过程是否达到了平衡状态还没有一个成熟的方法来解决，目前常见的方法是看是否状态已经平稳（例如画一个图，如果在较长的过程中，变化已经不大，说明很有可能已经平衡）当然这个方法并不能肯定一个状态是否平衡，你可以举出反例，但是却是实际中没有办法的办法。

随机模拟的基本思想和常用采样方法（sampling）