这种题一般有二种形式，共同点是都已知中序序列。如果没有中序序列，是无法唯一确定一棵树的。

<1>已知二叉树的前序序列和中序序列，求解树。

1、确定树的根节点。树根是当前树中所有元素在前序遍历中最先出现的元素。

2、求解树的子树。找出根节点在中序遍历中的位置，根左边的所有元素就是左子树，根右边的所有元素就是右子树。若根节点左边或右边为空，则该方向子树为空；若根节点

边和右边都为空，则根节点已经为叶子节点。

3、递归求解树。将左子树和右子树分别看成一棵二叉树，重复1、2、3步，直到所有的节点完成定位。

<2>、已知二叉树的后序序列和中序序列，求解树。

1、确定树的根。树根是当前树中所有元素在后序遍历中最后出现的元素。

2、求解树的子树。找出根节点在中序遍历中的位置，根左边的所有元素就是左子树，根右边的所有元素就是右子树。若根节点左边或右边为空，则该方向子树为空；若根节点

边和右边都为空，则根节点已经为叶子节点。

3、递归求解树。将左子树和右子树分别看成一棵二叉树，重复1、2、3步，直到所有的节点完成定位。

测试用例：

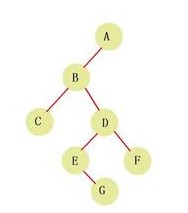
<1>先序 中序 求 后序

输入：

先序序列：ABCDEGF

中序序列：CBEGDFA

输出后序：CGEFDBA

代码：

/*
	PreIndex: 前序序列字符串中子树的第一个节点在PreArray[]中的下标
    InIndex:  中序序列字符串中子树的第一个节点在InArray[]中的下标
	subTreeLen: 子树的字符串序列的长度
	PreArray： 先序序列数组
	InArray：中序序列数组
*/
void PreInCreateTree(BiTree &T,int PreIndex,int InIndex,int subTreeLen){
	//subTreeLen < 0 子树为空
	if(subTreeLen <= 0){
		T = NULL;
		return;
	}
	else{
		T = (BiTree)malloc(sizeof(BiTNode));
		//创建根节点
		T->data = PreArray[PreIndex];
		//找到该节点在中序序列中的位置
		int index = strchr(InArray,PreArray[PreIndex]) - InArray;
		//左子树结点个数
		int LenF = index - InIndex;
		//创建左子树
		PreInCreateTree(T->lchild,PreIndex + 1,InIndex,LenF);
		//右子树结点个数(总结点 - 根节点 - 左子树结点)
		int LenR = subTreeLen - 1 - LenF;
		//创建右子树
		PreInCreateTree(T->rchild,PreIndex + LenF + 1,index + 1,LenR);
	}
}

主函数调用：

BiTree T;
	PreInCreateTree(T,0,0,strlen(InArray));
	PostOrder(T);

另一种算法：

/*
	PreS       先序序列的第一个元素下标
    PreE       先序序列的最后一个元素下标
	InS        中序序列的第一个元素下标 
	InE        先序序列的最后一个元素下标  
	PreArray   先序序列数组
	InArray    中序序列数组
*/
void PreInCreateTree(BiTree &T,int PreS ,int PreE ,int InS ,int InE){
	int RootIndex;
	//先序第一个字符
	T = (BiTree)malloc(sizeof(BiTNode)); 
	T->data = PreArray[PreS];
	//寻找该结点在中序序列中的位置
	for(int i = InS;i <= InE;i++){
		if(T->data == InArray[i]){
			RootIndex = i;
			break;
		}
	}
	//根结点的左子树不为空
	if(RootIndex != InS){
		//以根节点的左结点为根建树
		PreInCreateTree(T->lchild,PreS+1,(RootIndex-InS)+PreS,InS,RootIndex-1);
	}
	else{
		T->lchild = NULL;
	}
	//根结点的右子树不为空
	if(RootIndex != InE){
		//以根节点的右结点为根建树
		PreInCreateTree(T->rchild,PreS+1+(RootIndex-InS),PreE,RootIndex+1,InE);
	}
	else{
		T->rchild = NULL;
	}
}

<2>中序 后序 求先序

输入：

中序序列：CBEGDFA

后序序列：CGEFDBA

输出先序：ABCDEGF

代码：

/*
	PostIndex: 后序序列字符串中子树的最后一个节点在PreArray[]中的下标
    InIndex:  中序序列字符串中子树的第一个节点在InArray[]中的下标
	subTreeLen: 子树的字符串序列的长度
	PostArray： 后序序列数组
	InArray：中序序列数组
*/
void PostInCreateTree(BiTree &T,int PostIndex,int InIndex,int subTreeLen){
	//subTreeLen < 0 子树为空
	if(subTreeLen <= 0){
		T = NULL;
		return;
	}
	else{
		T = (BiTree)malloc(sizeof(BiTNode));
		//创建根节点
		T->data = PostArray[PostIndex];
		//找到该节点在中序序列中的位置
		int index = strchr(InArray,PostArray[PostIndex]) - InArray;
		//左子树结点个数
		int LenF = index - InIndex;
		//创建左子树
		PostInCreateTree(T->lchild,PostIndex - (subTreeLen - 1 - LenF) - 1,InIndex,LenF);
		//右子树结点个数(总结点 - 根节点 - 左子树结点)
		int LenR = subTreeLen - 1 - LenF;
		//创建右子树
		PostInCreateTree(T->rchild,PostIndex-1,index + 1,LenR);
	}
}

主函数调用：

BiTree T2;
	PostInCreateTree(T2,strlen(PostArray) - 1,0,strlen(InArray));
	PreOrder(T2);

完整代码：

#include<iostream>
#include<string>
using namespace std;

//二叉树结点
typedef struct BiTNode{
	//数据
	char data;
	//左右孩子指针
	struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

//先序序列
char PreArray[101] = "ABCDEGF";
//中序序列
char InArray[101] = "CBEGDFA";
//后序序列
char PostArray[101] = "CGEFDBA";
/*
	PreIndex: 前序序列字符串中子树的第一个节点在PreArray[]中的下标
    InIndex:  中序序列字符串中子树的第一个节点在InArray[]中的下标
	subTreeLen: 子树的字符串序列的长度
	PreArray： 先序序列数组
	InArray：中序序列数组
*/
void PreInCreateTree(BiTree &T,int PreIndex,int InIndex,int subTreeLen){
	//subTreeLen < 0 子树为空
	if(subTreeLen <= 0){
		T = NULL;
		return;
	}
	else{
		T = (BiTree)malloc(sizeof(BiTNode));
		//创建根节点
		T->data = PreArray[PreIndex];
		//找到该节点在中序序列中的位置
		int index = strchr(InArray,PreArray[PreIndex]) - InArray;
		//左子树结点个数
		int LenF = index - InIndex;
		//创建左子树
		PreInCreateTree(T->lchild,PreIndex + 1,InIndex,LenF);
		//右子树结点个数(总结点 - 根节点 - 左子树结点)
		int LenR = subTreeLen - 1 - LenF;
		//创建右子树
		PreInCreateTree(T->rchild,PreIndex + LenF + 1,index + 1,LenR);
	}
}
/*
	PostIndex: 后序序列字符串中子树的最后一个节点在PreArray[]中的下标
    InIndex:  中序序列字符串中子树的第一个节点在InArray[]中的下标
	subTreeLen: 子树的字符串序列的长度
	PostArray： 后序序列数组
	InArray：中序序列数组
*/
void PostInCreateTree(BiTree &T,int PostIndex,int InIndex,int subTreeLen){
	//subTreeLen < 0 子树为空
	if(subTreeLen <= 0){
		T = NULL;
		return;
	}
	else{
		T = (BiTree)malloc(sizeof(BiTNode));
		//创建根节点
		T->data = PostArray[PostIndex];
		//找到该节点在中序序列中的位置
		int index = strchr(InArray,PostArray[PostIndex]) - InArray;
		//左子树结点个数
		int LenF = index - InIndex;
		//创建左子树
		PostInCreateTree(T->lchild,PostIndex - (subTreeLen - 1 - LenF) - 1,InIndex,LenF);
		//右子树结点个数(总结点 - 根节点 - 左子树结点)
		int LenR = subTreeLen - 1 - LenF;
		//创建右子树
		PostInCreateTree(T->rchild,PostIndex-1,index + 1,LenR);
	}
}
//先序遍历  
void PreOrder(BiTree T){  
    if(T != NULL){  
		//访问根节点  
		printf("%c ",T->data);
        //访问左子结点  
        PreOrder(T->lchild);  
        //访问右子结点  
        PreOrder(T->rchild);   
    }  
}  
//后序遍历  
void PostOrder(BiTree T){  
    if(T != NULL){  
        //访问左子结点  
        PostOrder(T->lchild);  
        //访问右子结点  
        PostOrder(T->rchild); 
		//访问根节点  
		printf("%c ",T->data);
    }  
}  
int main()
{
	BiTree T;
	PreInCreateTree(T,0,0,strlen(InArray));
	PostOrder(T);
	printf("\n");
	BiTree T2;
	PostInCreateTree(T2,strlen(PostArray) - 1,0,strlen(InArray));
	PreOrder(T2);
    return 0;
}

二叉树先序序列和中序序列求解树