1、问题描述

在 OSC 问答频道有一个问题：时间算法:帮忙解答下

简单的复述一遍就是能够通过如下式子来计算month月day日是一年的第几天。

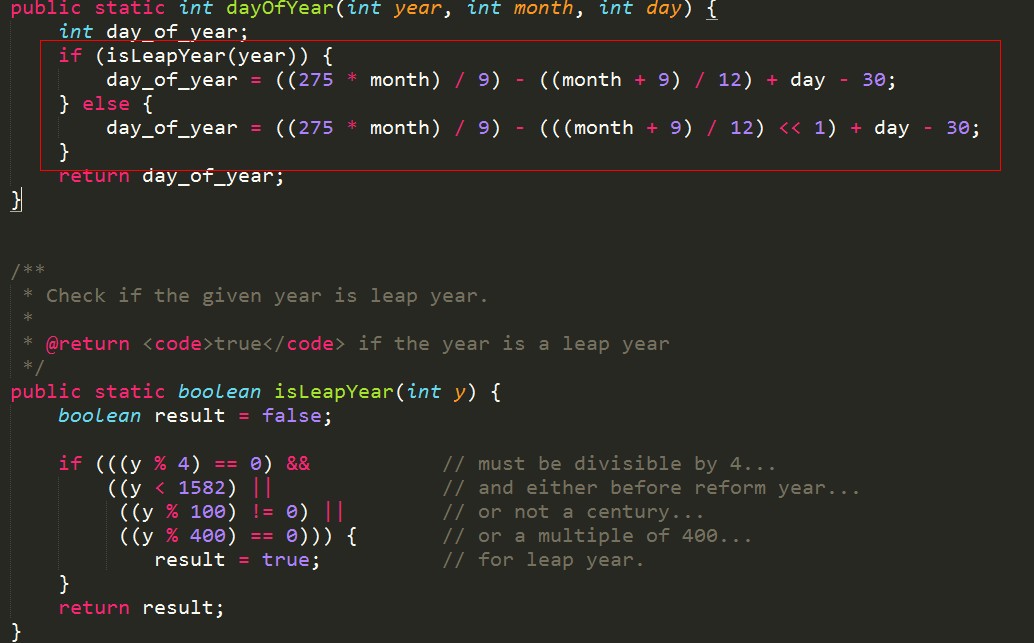
闰年是 day_of_year=(275*month)/9 - (month+9)/12 + day - 30

非闰年比这个少1天。可以简单的验证，这个式子中每个部分计算后都取整，整个结果总是对的。

我们知道1、3、5、7、8、10、12都是31天，2月的天数有点诡异，其他都是30天，正常情况下我们写程序会写很多if来判断月份，进而计算累积的天数。但是为什么这个式子不用if就搞定了呢？式子中很奇怪的275、9、12，都是这么来的呢？

2、原理分析

简单的分析下，式子可以变形为：

day_of_year=【(275*month)/9 - 30】 - 【(month+9)/12】 + 【day】

 =【30*（month-1）】+ 【5*month/9】+【day】-【（month+9）/12】 

这样可以把式子分成4个部分，我们一一来解释这四个部分的含义：

part1：30*（month-1）

part2：5*month/9

part3：day

part4：（month+9）/12

1）我们知道，计算x月y日的天数，实际上真正需要计算的就是前面(x-1)个月的天数之和，加上y，即可。

这里的y就是part3中的day。

2）然后我们只需要计算前面的(x-1)个月的天数之和了。

我们可以先假设每个月都只有30天，然后计算正三五七八十腊多出来的1天（下面第四条）和二月不足30的天数（下面第二条），合起来就是准确的天数了。假设每个月都是30天，那么一共就是30*(x-1) 天，这就是part1。

3）对闰年来说，2月29天，比30天少1天，但是呢，只有x大于等于3的时候，天数里才包含这个29，所以找一个大于等于3的时候等于1的式子就可以了。比如当前的例子中用的是part4，即（month+9）/12。同理，用（month+8）/11、或（month+7）/10其实也一样。（month+6）/9就不行了，因为month=12时，它等于2了。

4）最后我们再来分析正三五七八十腊这些大月多出来的1天。

我们可以先统计一下每个月之前所有的大月累积多出来的一天之和sum。例如5月份的话，前面有1、2、3、4四个月，只有1、3月是大月比30天多1天，所以sum=2.对应的表格如下：

x   =>  sum

1   => 0

2   => 1

3   => 1

4   => 2

5   => 2

6   => 3

7   => 3

8   => 4

9   => 5 （规则开始变化、发生了“跃迁”）

10  => 5

11  => 6

12  => 6

如果有个函数能表示这个sum(x)，就可以直接用来计算多出来的天数了。

这个函数有个特点，在x小于9的时候，值为x/2取整; 在x大于等于9、小于等于12的时候，值为(x+1)/2取整。

恰好part2，即5*x/9 取整可以满足这一点（不信可以自己计算下）。类似的式子可以找出来很多，但是可以证明分母最小的就是5/9;也可以证明如果“跃迁”发生在sum(8)=5或者sum(7)=4，那么对应的函数可以是5/8*month, 4/7*month。

我们也可以注意到，函数值近似于1/2，而5/9也差不多就是1/2。

一个整数x乘以1/2，其小数部分要么为0(x为偶数的时候)，要么为1/2（x为奇数的时候）。

而5/9比1/2大1/18，所以x小于9的时候，5/9*x的值与x/2的值之差，一直小于9/18=1/2，他们取整是相等的（小数部分小于1/2+1/2=1）。

而在x大于等于9的时候，差值>=9/18=1/2了，所以，x为偶数的时候，函数值为x/2，为奇数的时候，变成x/2+1。

这两个合并到一起就是(x+1)/2取整。所以part2即可以用来表示sum(x). 把part1、part2、part3、part4合起来就是准确的天数了。

类似的，式子part2可以用5/9到5/8之间的任何分数代替，例如51/90*month，50/89*month...等等。 

当然这里讨论的都是不用if判断，直接表达出来的方式，如果可以用一个if判断，最简单的是：

如果小于8，直接除以2取整；否则，加1除以2取整。