首页 > 代码库 > 贪心思维 专题记录 2017-7-21
贪心思维 专题记录 2017-7-21
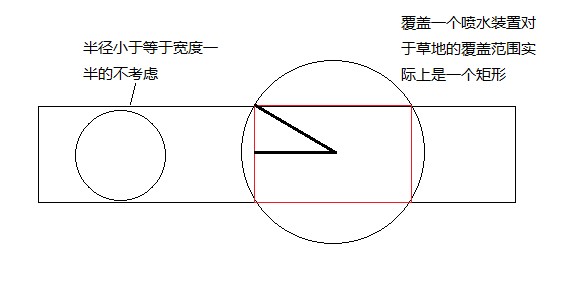
A、UVa 10382 - Watering Grass

#include <bits/stdc++.h>using namespace std;const int maxn = 10000+10;typedef pair <int,int > pii;typedef pair <double ,double >pdd;struct p{ double a,b;};int n;double l,w;pdd s[maxn];bool cmp(const pii &x,const pii &y){ if(x.first != y.first) return x.first < y.first; return x.second < y.second;}int solve(){ int cnt = 0; double last = 0,far = 0; for(int i=0;i < n;i++) { if(last >= l) return cnt; if(s[i].first <= last) far = max(far,s[i].second); else if(s[i].first > last) { cnt++; last = far; if(s[i].first <= last) far = max(far,s[i].second); else return -1; } } if(last < l && far >= l) return cnt+1; if(far < l ) return -1; return cnt;}int main (){ while( scanf("%d%lf%lf", &n, &l, &w) != EOF) { for(int i=0;i < n;i++) { double pos , r; scanf("%lf %lf",&pos,&r); double d = sqrt(1.0*r*r-w*w/4.0); s[i].first = pos - d, s[i].second = pos + d; } sort(s,s+n,cmp); cout<< solve()<<endl; } return 0;}
B、UVa 10905 - Children‘s Game
题目大意:
给出n个数字 输出组合最大的
思路 :两个数 如果位数相同 直接比较大小 ;
如果不同 就两个数换位置 看哪个大;

#include <iostream>#include <algorithm>#include <string>#include <string.h>using namespace std;string s[60];bool cmp(const string &a,const string &b){ if(a.size() == b.size()){ return a < b; } string t1 = a+b, t2=b+a; return t1 < t2;}int main(){ int n; while (cin >> n && n) { for(int i=0;i<n;i++) cin >> s[i]; sort(s,s+n,cmp); for(int i=n-1;i>=0;i--) cout<< s[i]; cout<<endl; } return 0;}
C、UVA 11134 Fabled Rooks
题目大意:
在一个n*n(1<=n<=5000)的棋盘上放置n个车,每个车都只能在给定的一个矩形里放置,使其n个车两两不在同一行和同一列,判断并给出解决方案
思路 :把题目里的二维的改成一维的,就是有一行,让你放,每个车可以放一个区间[li,ri],让你找一种方案,使得每个车不在同一个格子里。然后就可以这样贪心:枚举每个格子,记为i,那么是不是所有满足左端点li <= i的里头,挑一个右端点尽可能小的来放在这一个格子里面?,因为右端点越大,它后面可 能可以放的格子越多,越小,可放的格子越小,所以我们这样贪心的来放

#include <bits/stdc++.h>using namespace std;const int mod = 1e9 + 7;const int maxn = 5000 + 10;const int INF = 0x3f3f3f3f;typedef long long LL;typedef pair <int ,int > pii;typedef pair <LL ,LL >pLL;typedef unsigned long long ull;struct node { int left,ri,order; bool operator < (const node & l)const{ if(left != l.left) return left < l.left; return ri < l.ri; }} x[maxn],y[maxn];int X[maxn],Y[maxn];bool solve (int n,node s[],int S[]){ sort(s,s+n); priority_queue <pii,vector<pii>,greater<pii> > q; int cnt =0, ret = 0; for(int i=1;i <= n;i++) { while (cnt < n && s[cnt].left <= i)//不停找左边界 { q.push( pii(s[cnt].ri,s[cnt].order) );//右边的边界 压进来 cnt++; } if(q.size() == 0) return 0; pii p =q.top(); if(p.first < i) return 0; //右边界如果小于i的话 已经找不到了 S[p.second] = i; q.pop(); ret++; // cout << ret <<endl; } return ret == n;}int main (){ int n; while (~scanf("%d",&n) && n) { for(int i=0;i < n;i++) { scanf("%d%d%d%d",&x[i].left, &y[i].left , &x[i].ri, &y[i].ri); x[i].order = y[i].order = i; } if( solve (n,x,X) && solve (n,y,Y) ) { for(int i=0; i < n;i++) { printf("%d %d\n",X[i],Y[i]); } } else printf("IMPOSSIBLE\n"); } return 0;}
D、uva 11100 - The Trip
题目大意:
有很多包,已知包的区别只在于高度不一样,小包可以装到大包里边,求最终剩下多少个包,并输出没一个组合
思路 :相同的包裹没办法在一个组里面 所以最后剩下的包 即为最大的 相同的包的 个数 k;
然后按照大小排序,然后每隔k个间隔选一个数 构成一个组别 example:x,x+k,.....x+t*k (x+t*k <= n)

#include <bits/stdc++.h>using namespace std;const int maxn = 10000+10;int s[maxn];int num[1000010];int main (){ int n; while (cin >> n && n){ int k = 0; memset(num,0,sizeof(num)); for(int i=0;i<n;i++){ cin >> s[i]; num[s[i]] ++; k = max(k,num[s[i]]); } cout<< k <<endl; sort(s,s+n); for(int i=0;i<k;i++) { cout<< s[i]; for(int j=k+i;j<n;j+=k){ cout<< " "<<s[j]; } cout<< endl; } //cout<<endl; } return 0;}
E、UVa 11384 - Help is needed for Dexter
题目大意:
给你1~n,n个连续的整数,每次可以从里面取出人一个数字减去一个任意数, 问最少操作多少次可以全变成0。
思路 : 本题思路就是每次都找中间的那个 然后直接减掉 比如 1 2 3 4 5 就找 3 然后剪掉3 就变成 1 2 0 1 2
然后 接着就变成了 1 2 依次递减

#include <bits/stdc++.h>using namespace std;int main (){ int n; while (cin >> n) { int cnt = 0; while (n > 0 ) { n/=2; cnt++; } cout<<cnt<<endl; } return 0;}
F、UVa 10795 A Different Task
题目大意:
有三个柱子 然后给你初始 和 目标的盘子所在的柱子 求最小移动次数
思路 :
参照 http://www.cnblogs.com/arbitrary/archive/2012/12/11/2813245.html
就是 首先找最大不在目标柱子上的盘子K 之前已经就位了 不用动
然后 转换成 一个大概的状态: 只有K 在 初始盘 然后 其余的k-1个都在中转盘上 然后 想把K 移动到 除了第三个盘上
所以问题变成答案=从初始局面移到参考局面步数+目标局面移到参考局面步数+1;

#include <iostream>#include <cstring>#include <string.h>#include <cstdio>#include <cmath>#include <algorithm>using namespace std;const int mod = 1e9 + 7;const int maxn = 70;const int INF = 0x3f3f3f3f;const double eps = 1e-8;typedef pair<int, int>pii;typedef pair<double, double>pdd;typedef long long LL;typedef unsigned long long ull;int s[maxn],e[maxn];LL f(int *p,int i,int final){ if ( i == 0) return 0; if(p[i] == final) return f(p,i-1,final); return f(p,i-1,6-final-p[i]) + (1LL << (i-1));//将i-1个盘子 从中转柱子 移动到本来的位置 所以加上2的i-1次方}int main(){ int n; int Case =1; while (~scanf("%d",&n), n) // 有n个盘子 { for(int i=1;i<=n;i++) cin >> s[i]; for(int i=1;i<=n;i++) cin >> e[i]; int k = n; while(s[k] == e[k] && k) k--; LL ans = 0; if( k != 0) { int other = 6-s[k] - e[k];//找到中转的柱子 ans = f(s,k-1,other) + f(e,k-1,other) + 1;//把1到k-1移到中转柱子上 然后再将k移动到目标柱子 } printf("Case %d: %lld\n",Case++,ans); } return 0;}
G、UVA 11520 - Fill the Square
题目大意:
给你一个n*n的格子,有些里面有大写字母,用大写字母填满格子,相邻的格子中字母不相同, 并且使得从上到下,从左到右的字母字典序最小。
思路 : 构造。将格子从上到下,从左到右编号,然后按编号填充,避免冲突即可,这样一定最小。
(如果,该方案不是最小,那么之前一定会选择更小的方案,而不是本方案)

#include <iostream>#include <cstring>#include <iostream>#include <cstdio>using namespace std;const int maxn = 15;char s[maxn][maxn];int main (){ int t,n; cin >> t; //100 * 100 *26 for(int a=1;a<=t;a++) { cin >> n; for(int i=0;i<n;i++) cin >> s[i]; for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { if(s[i][j] == ‘.‘) { for(char k = ‘A‘;k<=‘Z‘;k++) { bool ok = 1; if(i > 0 && s[i-1][j] == k) ok=0; if(i < n-1 &&s[i+1][j] == k ) ok=0; if(j > 0 && s[i][j-1] == k) ok=0; if(j< n-1 && s[i][j+1] == k) ok = 0; if( ok ) { s[i][j] = k; break; } } } } } printf("Case %d:\n",a); for(int b=0;b<n;b++) cout<< s[b]<<endl; } return 0;}
贪心思维 专题记录 2017-7-21

