给定多边形的顶点坐标（有序），让你来求这个多边形的面积，你会怎么做？
我们知道，任意多边形都可以分割为N个三角形，所以，如果以这为突破点，那么我们第一步就是把给定的多边形，分割为数个三角形，分别求面积，最后累加就可以了，把多边形分割为三角形的方式多种多样，在这里，我们按照如下图的方法分割：

图1

S点作为起始点（点1），a->e依次作为点2,3……。
一个三角形的面积是怎样的呢？
根据线性代数的知识，我们有如下的三角形面积公式，称之为有向面积(signed area)：

将这个行列式以第三列展开可以得到：

这就是以点1、2、3构成的三角形的有向面积（点如果是顺时针给出，有向面积为负，逆时针给出，有向面积为正），那么继续我们的工作，通过三角形的面积公式，来得到多边形的面积公式：
对于图1而言，多边形的面积就是：
S(1->6)=S(1,2,3)+S(1,3,4)+S(1,4,5)+S(1,5,6)
这里我们不免有些疑问，第一，图1所给出的是凸多边形，那这种算法对于非凸多边形是否同样适用呢？比如下面这个最简单的凸多边形的图形：

图2

用刚才的划分方法的话，就会出现一个诡异的问题，那就是有一个三角形出现在了图形的外面，而另外一个又超出了多边形的范围（划分为了Sab，Sbc两个图形），那么这样再用刚才的公式求面积，结果还是正确的么？
S(1->4)=S(1,2,3)+S(1,3,4)
先公布结论，这个式子是正确的，等等，为什么？还记得刚才我提到了那个“有向面积”的概念么？忘了的话，请回头看看加重了的字。
请注意从图中看，Sab点为顺时针排列，Sbc点为逆时针排列，面积从数值上就是从Sab这个超过范围的大三角形中去掉Sbc这个小三角形，最后的结果神奇的就是多边形Sabc的面积，那么这个结论能否推广到任意多边形呢？

图3

在这里不做证明，下面给出的公式，就是任意多边形的面积公式：

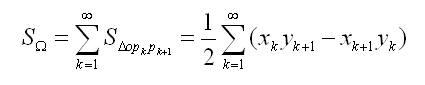
例题：

Input

输入数据包含多个测试实例，每个测试实例占一行，每行的开始是一个整数n(3<=n<=100)，它表示多边形的边数（当然也是顶点数），然后是按照逆时针顺序给出的n个顶点的坐标（x1, y1, x2, y2... xn, yn）,为了简化问题，这里的所有坐标都用整数表示。 
输入数据中所有的整数都在32位整数范围内，n=0表示数据的结束，不做处理。 

 

Output

对于每个测试实例，请输出对应的多边形面积，结果精确到小数点后一位小数。 
每个实例的输出占一行。 

 

Sample Input

3 0 0 1 0 0 14 1 0 0 1 -1 0 0 -10

 

Sample Output

0.52.0

 

 代码：

#include<cstdio>#include<cmath>int main(){     int n;     int p[110][2];     while(scanf("%d",&n)&& n){          for(int i = 0; i < n; i ++)          scanf("%d%d",&p[i][0],&p[i][1]);          p[n][0] = p[0][0];          p[n][1] = p[0][1];          int s = 0;          for(int i = 0; i < n; i ++){               s += (p[i][0]*p[i+1][1] - p[i+1][0]*p[i][1]);          }          printf("%.1lf\n",s/2.0);     }return 0;}

View Code

注意上面的公式是循环一周的，最后Xn*Y1-X1*Yn也要加进去 = =