首页 > 代码库 > 浅析B树结构
浅析B树结构
B树简介
B树，是为磁盘或其他直接存取辅助存储设备二设计的一种平衡查找树，由于它的特殊结构，可以大大减少访问磁盘I/O的次数，因此在数据库系统常使用Ｂ数或Ｂ树的变形来存储信息。
Ｂ树满足某种条件，与红黑树或其他搜索树不同，一棵M（M>2）的B树，是一棵M路的平衡搜索树，它允许有多条分支子树，它可以是一条空树，或者满足以下性质：
1、根节点至少有两个孩子
2、每个非根节点有[ M/2，M ]个孩子
3、每个非根节点有[ (M/2) -1，M-1 ]个关键字，并且以升序排序
4、key[i]和key[i+1]之间的孩子节点的值介于两者之间
5、所有的叶子节点都在同一层
B树是一棵向上生长的树，当一个节点中的关键字个数达到上限之后，会进行分裂，同时会向上产生一个新的节点，分裂得到两个子节点和一个父节点，父节点只有原来节点中的中间key值，两个子节点将平分原来节点中剩下的key和孩子。这些原因使得B树满足上述条件2~5。接下来看张图，理解一下B树是如何生长的。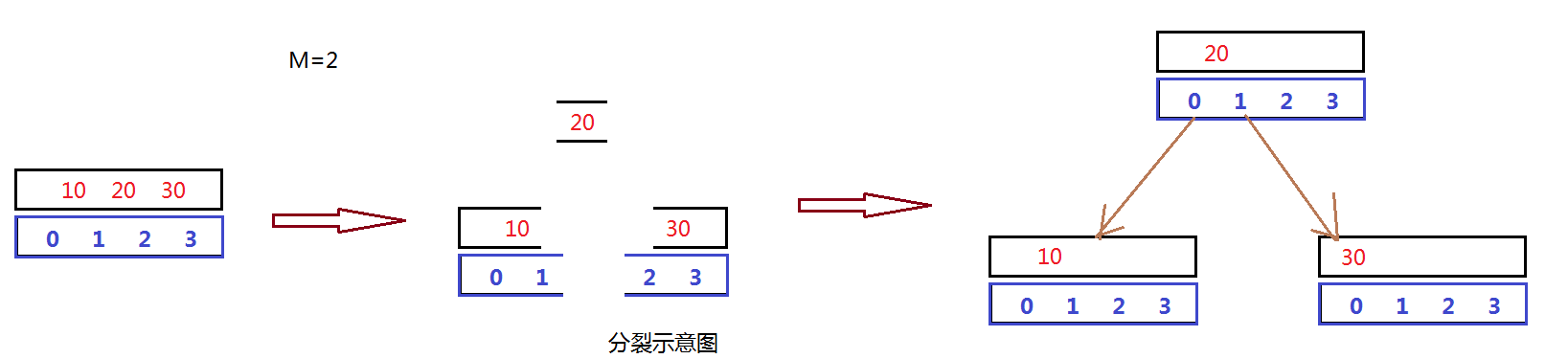
没有完全看明白先放下，这里只需要知道B树是一棵多路的平衡搜索树。在树不为空树的前提下，如果M=2，那么所有节点内最多会有M-1个关键字key值，每个节点都会有M个孩子。在一个节点内，关键字是从小到大排列的，关键字和孩子是插空分布的，这也保证了B树的平衡搜索性。
接下来通过B树的基本算法来了解一下树。
B树算法
关键字：分裂算法、插入算法、查找算法、中序遍历算法
首先，根据上述B树的要求，这里给出一张B树的示意图（M=3）
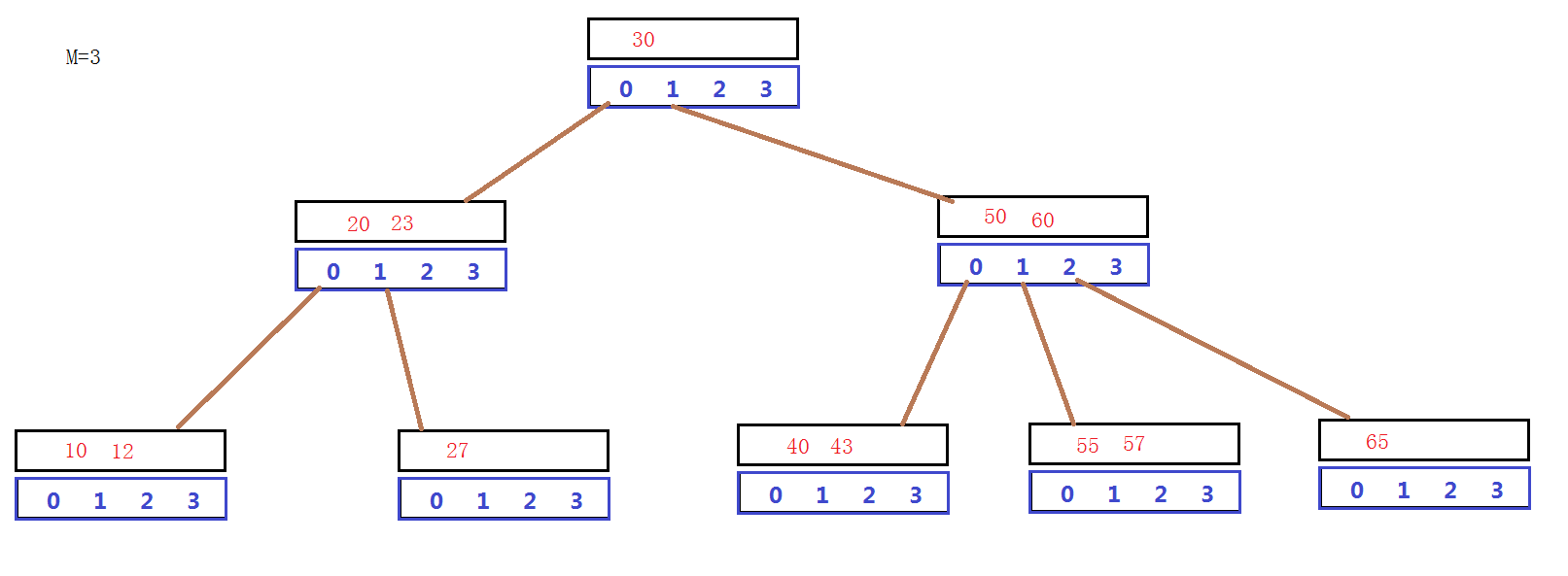上面说过，M表示的是每个结点孩子的个数，但是很明显，在上图中，孩子给出了4个，那么对应的关键字会有3个，和一开始的理论不相符。这里需要说明一下，因为每次向B树中插入节点之后，会进行判断，该节点的关键字个数是否超过了M，如果超过，我们需要进行分裂算法（后面会提到）。
经过简单分析，这里给出B树的节点的定义及构造函数。
template <typename K,int M>
struct BTreeNode
{
K _key[M];//关键字数组
BTreeNode<K,M>* _sub[M+1];//指向孩子节点的指针数组
BTreeNode<K,M>* _parent;//指向父节点的指针
size_t _size; //该节点中已经插入的关键字的个数
BTreeNode()
:_parent(NULL)
,_size(0)
{
size_t i = 0;
for(i = 0; i < M; i++)
{
_key[i] = K();
_sub[i] = NULL;
}
_sub[i] = NULL;
}
}第一步：查找算法 Find()
为什么这里要先来实现B树的查找呢？因为对一棵树的查找来说，并不会影响到树的结构，另外，通过查找，也可以帮助我们得到一些其他的更有利的信息，方便其他功能的实现。
以上面给出的B树为例，在B树中查找一个结点，和普通的平衡树基本思路一样，比该点的key大就向右查找，比该点的key值小，就向左查找。只不过对于B树而言，每个节点有M-1个关键字。因此在向下查找的同时，需要对每个节点中的每个key进行比较。
由于每个节点这里有M个关键字，下标从0~M-1，每个节点有M+1个孩子，指针数组的下标从0~M，仔细观察上树，对于某个节点node而言，比节点中的某个key小的一个值，下一次查找的孩子应该和该key的下标相同。
还需要注意的一点，就是我这里的Find函数是希望能够被其他函数使用的，不仅仅是希望得到一个bool值或找到的Node*，在这里设计Find函数，是希望当找到该key值的话返回key所在节点的下标，同时返回一个指向该节点的指针；没有找到返回 -1，同时返回该节点应该所在位置的父节点。初衷很简单，是为了给待会需要实现的Insert函数调用，达到代码的复用性。如果我们只是判断该节点在不在B树内，那对返回值我们就只需要关注bool即可。要实现返回两个参数，有两种思路：第一就是通过函数传参数的方式，传递引用达到目的，第二就是使用pair类型。
Pair是库中定义好的一个双变量结构体，这里给出库中pair的实现
template<class _Ty1,class _Ty2>
struct pair
{// store a pair of values
typedef _Ty1 first_type;
typedef _Ty2 second_type;
}下面是Find函数的实现代码：
typedef pair<Node*, int> FindType;
FindType Find(const K& key)
{
Node* parent = NULL;
Node* cur = _root;
while(cur)
{
size_t i =0;
while(i < cur->_size)
{
if(key > cur->_key[i])
{
i++;
}
else if(key < cur->_key[i])
{
break;
}
else
{
return FindType(cur, i);
}
}
parent = cur;
cur = cur->_sub[i];
}
return FindType(parent,-1);
}第二步：插入算法 Insert()与分裂
插入算法应该是比较复杂的了。
我们先考虑这样一个问题，当插入一个元素之后（树不为空树），应该会有两种情况，一种是该节点中关键字的个数并没有超过或等于M，这个时候完全不需要调整，可以直接结束。另一种情况，也就是我们需要考虑的，当插入一个关键字之后，该节点的key满了，这时候，就需要用到分裂算法。
我们来考虑，在下图中的B树中插入56，会发生哪些事。
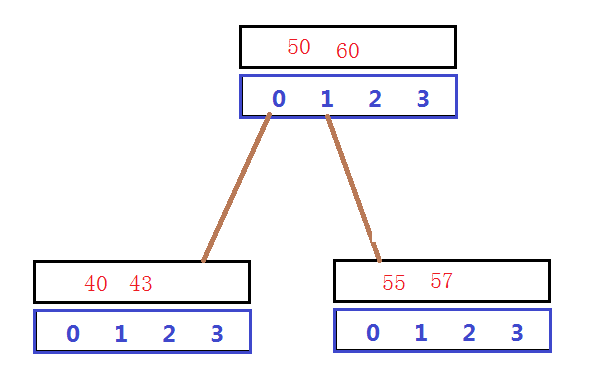
首先，我们应该先找到56应该插入的位置。这里Find()函数就可以帮得上忙。如果Find查找到了该key，就不需要再插入，如果没有找到，返回最终找到空节点的父节点，直接在该节点中插入即可。在上图中，用Find()函数查找56，返回的指针应该是指向右下角的结点，接下来开始插入节点。
需要注意的是，这里把56插入之后，还做了件其他的事，57的左右孩子也跟着向右移动，因为它的左右孩子都是空结点，因此这里并没有直接画出来。
接下来的任务就是开始分裂。
对B树的分裂，实际上是将关键字超出M-1的节点的中间关键字提取出来，同时将两侧分成两个子节点。注意，这里只是把中间的关键字取出来，然后把中间的关键字再次插入到它的父节点中，同时将分裂产生的的新节点连接到父节点上。连接到父节点上的位置，与向父节点中插入新的关键字的位置有关，如图：
调整之后如果发现，父节点的关键字个数又超出了范围，如上图，则再向上分裂增长，直到某一次插入之后，关键字的个数不超过M-1，则停止分裂并返回，或者某次分裂到根节点之后，对根节点特殊处理，之后直接结束程序。这就是分裂算法。
多注意一点的是，我们第二次插入的过程中，插入了key值，同时将分裂产生的节点也连接到了父节点上，因此，这里对插入key的过程做了一次封装，实现如下：
void InsertKey(Node* node, const K& key, Node* sub)
{
size_t index = node->_size-1;
// 比key小的关键字连带孩子节点同时向后移动
while (index >= 0)
{
if (node->_key[index] > key)
{
//向后移动
node->_key[index + 1] = node->_key[index];
node->_sub[index + 2] = node->_sub[index + 1];
}
else // (node->_key[index] < key)
{
break;
}
--index;
}
// 将key插入到node结点当中
node->_key[index + 1] = key;
// 将分裂产生的结点连接在node节点上
node->_sub[index + 2] = sub;
if (sub != NULL)
sub->_parent = node;
// 对node的size调整
node->_size++;
}下面是插入节点实现代码：
bool Insert(const K& key)
{
// 树是空树
if (_root == NULL)
{
_root = new Node;
_root->_key[0] = key;
_root->_parent = NULL;
_root->_size = 1;
return true;
}
// 在树中Find该结点
FindNode ret = Find(key);
if (ret.second != -1) // 树中找到该节点
return false;
Node* cur = ret.first;
Node* parent = cur->_parent;
Node* sub = NULL;
int newkey = key;
while (1)
{
//在 cur 节点里面插入key、sub
//如果cur没满，跳出循环
//cur->key满了，向上分裂
InsertKey(cur, newkey, sub);
if (cur->_size < M)
return true;
//开始分裂
size_t mid = cur->_size / 2;
newkey = cur->_key[mid]; // 获取下一次要插入的值
Node* tmp = new Node;
size_t j = 0;
size_t i = 0;
size_t sz = cur->_size;
for (i = mid + 1; i < sz; i++)
{
tmp->_key[j] = cur->_key[i];
tmp->_sub[j] = cur->_sub[i];
//注意子节点的父指针
if (tmp->_sub[j])
tmp->_sub[j]->_parent = tmp;
j++;
tmp->_size++; // 调整size
cur->_size--;
cur->_key[i] = K(); // 将cur分裂出去的部分恢复默认值
cur->_sub[i] = NULL;
}
tmp->_sub[j] = cur->_sub[i];
//注意子节点的父指针
if (tmp->_sub[j])
tmp->_sub[j]->_parent = tmp;
cur->_sub[i] = NULL;
// 清空原来的key[mid]结点
cur->_key[mid] = K();
cur->_size--;
//根节点
if (parent == NULL)
{
_root = new Node;
_root->_key[0] = newkey;
_root->_size = 1;
_root->_sub[0] = cur;
_root->_sub[1] = tmp;
cur->_parent = _root;
tmp->_parent = _root;
return true;
}
//非根节点
cur = parent;
parent = parent->_parent;
sub = tmp;
}
return true;
} 要实现插入算法，就是要通过分裂实现，通过判断结点关键字的个数，决定是否分裂，分裂就是以中间的关键字为断点，一分为二，提出中间关键字继续向上插入。两个分节点连接到上一层结点。
第三步：中序遍历算法
之所以要实现中序遍历，是因为对于一棵平衡搜索树而言，中序遍历的结果是有序的，中序遍历采用递归实现并不难，但要注意的一个问题是对每个key进行访问的同时，我们不能再对两个孩子进行递归访问，因为这会对中间的孩子访问两次。如下图：
对中间的结点访问了两次，因此在普通二叉搜索树上除了要增加对每个结点中key的访问，也要禁止对左右子树都遍历，于是有如下实现代码：
// 实现代码 1
void _InOrder(Node* root)
{
if (root == NULL)
return;
size_t i = 0;
for (i = 0; i < root->_size; i++)
{
_InOrder(root->_sub[i]);
cout << root->_key[i] << " ";
}
_InOrder(root->_sub[i]);
}// 实现代码 2
void _InOrder(Node* root)
{
if (root == NULL)
return;
for (size_t i = 0; i < root->_size; i++)
{
_InOrder(root->_sub[i]);
cout << root->_key[i] << " ";
//遍历过程中存在冲突，因为存在两个指针指向一个结点的情况
//解决方案：只打印前一半，到最后一个key的时候再打印后一半
if (i == root->_size-1)
_InOrder(root->_sub[i + 1]);
}
}关于测试用例，最直接的就是直接插入1到20，经过测试，1~20 依次插入，包含了所有情况，如果中序遍历可以有序输出，那么表明B树的实现基本已经可以满足要求。
B树及B树的变形，都是减少为了对磁盘的操作，上面看到当我们插入多个节点，它会进行多次的分裂，但当我们把M放到很大，那么它的高度就会成M的指数下降。
当 M=1024 的时候，三层可以容纳10亿个结点，换句话说，10亿结点我们只需要查找三次，对于每个节点中的key值，因为是有序的，采用二分查找不过10次，因此，在查找速度上是非常快的，也就减少了访问磁盘的次数。
对B树的应用，主要都体现在B树的变形上的应用，这也是大多数数据库设计的底层实现。
本文出自 “暮回” 博客，请务必保留此出处http://muhuizz.blog.51cto.com/11321490/1873257
浅析B树结构