2105. 最大矩形

Description

cs的妈妈买回来好多好多很长的纸条，这些纸条的宽度都是1，长度不同。淘气的cs把这些纸条剪了好多刀变得乱七八糟。

cs看到这么多长长短短的纸条实在是无聊，于是把这些纸条全都摆了起来，变成下图：

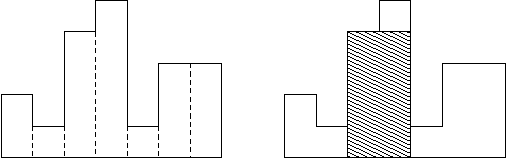
摆成的纸条如左图，现在cs想知道其中最大的矩形是什么（如右图阴影部分），请你告诉她这其中最大的矩形面积是多少。

Input Format

第一行，一个整数N，表示有N个纸条。 第二行，N个用空格隔开的整数h1,h2,?,hn,表示每个纸条的长度

Output Format

一行，最大矩形的面积大小

Sample Input

7
2
1
4
5
1
3
3

Sample Output

8

Sample Input

4
1000
1000
1000
1000

Sample Output

4000

About Testdata

20%的数据，N≤100

40%的数据，N≤1000

100%的数据，N≤100,000,0<hi<1,000,000,000

Limits

Time limit: 1000ms, memory limit: 65536kb.

=====题解正文===  

1. 题目解读：

1. 这道题目比较简单，用普通的做法来回扫两遍计算一下就能过，不过后来了解到有o（n）的写法于是学习了一下试着把这个方法些粗来。

2. 题目的数据用long long 就能过，不用写高精度。

3. 当我们扫到某个柱子时只要保证当前维持着最大矩形，面对下一个柱子再进行更新就好了。

2. 解题方法：

1. 我们考虑一个单调递增的柱状图，那么很显然，最大矩形的面积可以通过一遍扫描算出来。

2. 我们利用这个特性，时刻维护一个单调递增的柱状图，只要维护这一个过程的时间复杂度不高总算法的时间复杂度就是o(n)

3. 这个算法巧妙地运用了【栈】这一思想，维持栈顶的是最高的柱子。即遇到柱子i就判断长度是否大于栈顶，如果比栈顶大就加入栈，否则就push直到栈顶不大于当前柱子的高度，然后进入栈。

4. 在这一过程中我们需要计算出当前的最大值。

3. 代码

1. #include <iostream>
   #include <stack>
   using namespace std;
    
   long long n, rect[1000005];
   stack<int> s;
   long long area(0);
   int main()
   {
   	cin >> n;
   	for (int i = 0; i < n; ++i)
   		cin >> rect[i];
   	rect[n] = 0;//在最后添加一个0，为了后期闭合这个栈。
   	for (int i = 0; i <= n; ++i)
   	{
   		if (s.empty() || rect[s.top()] < rect[i])s.push(i);
   		else
   		{//计算最大值
   			int tmp = s.top();
   			s.pop();//弹出
   			long long temp = rect[tmp] * (s.empty() ? i : i - s.top() - 1);
   			if (area < temp)area = temp;
   			--i;
   		}
   	}
   	cout << area;
   }

SJTU OJ 2105 最大矩形