首页 > 代码库 > 分治策略
分治策略
1、二分查找
(1)、二分查找递归实现
#include<stdio.h>
#define NOT_FOUND -1;
int binSearch(int *a, int head, int tail, int key);
int binSearch(int *a, int head, int tail, int key){
int middle;
if(head <= tail){
middle = (head + tail)/2;
if(key == a[middle]){
return middle;
}
if(key < a[middle]){
return binSearch(a, head, middle-1, key);
}
if(key > a[middle]){
return binSearch(a, middle+1, tail, key);
}
}
return NOT_FOUND;
}
void main(void){
int a[] = {2, 3, 4, 6, 8, 10};
int count = sizeof(a)/sizeof(int);
int index;
int number;
printf("请输入要查找的数字: ");
scanf("%d", &number);
index = binSearch(a, 0, count-1, number);
printf("%d\n", index);
}(2)、结果截图
(3)、二分查找非递归实现
#include<stdio.h>
#define NOT_FOUND -1
int binSearch(int *a, int count, int key);
int binSearch(int *a, int count, int key){
int head = 0;
int tail = count-1;
int middle = (head+tail)/2;
while(head <= tail){ //有可能head和tail到达了同一个数字;
if(key < a[middle]){
tail = middle-1;
}else if(key > a[middle]){
head = middle+1;
}else{
return middle;
}
middle = (head+tail)/2;
}
return NOT_FOUND;
}
void main(void){
int a[] = {1, 3, 6, 8, 9, 10};
int count = sizeof(a)/sizeof(int);
int number;
int index;
printf("请输入要查找的数字:");
scanf("%d", &number);
index = binSearch(a, count, number);
printf("%d\n", index);
}(4)、结果截图
(5)、算法分析
时间复杂度为:O(logn);
2、乘方问题,给你一个数X,然后在给你一个正整数n,计算x的n次方?
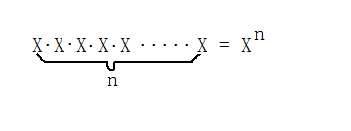
时间复杂度为:O(n);
怎么用分治法,在非线性时间内解决这个问题?
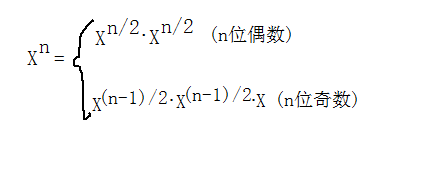
分解为2个子问题是完全一样的,所以时间复杂度为:O(logn);
3、斐波那契数列:输入n,求第n项?
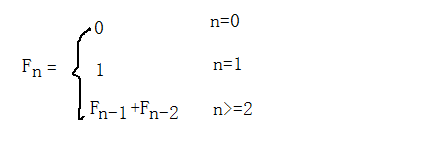
(1)、递归代码实现
#include<stdio.h>
int fibonacci(int n);
int fibonacci(int n){
if(n <= 0){
return 0;
}
if(n == 1){
return 1;
}
return fibonacci(n-1)+fibonacci(n-2);
}
void main(void){
int number;
int value;
printf("请输入斐波那契数:");
scanf("%d", &number);
value = fibonacci(number);
printf("%d\n", value);
}算法分析:
这就是一个递归树,处理相同的子问题,用的分治策略,在递归树上好多都是重复计算的;
时间复杂度(指数级):

(2)、非递归算法
#include<stdio.h>
int fibonacci(int n);
int fibonacci(int n){
int firstNumber = 0;
int secondNumber = 1;
int finNumber;
int i = 2;
if(n == 1){
return firstNumber;
}
if(n == 2){
return secondNumber;
}
for(i = 3; i <= n; i++){
finNumber = firstNumber + secondNumber;
firstNumber = secondNumber;
secondNumber = finNumber;
}
return finNumber;
}
void main(void){
int number;
int value;
printf("请输入第几个斐波那契数:");
scanf("%d", &number);
value = fibonacci(number);
printf("%d\n", value);
}算法分析:
时间复杂度:O(n);
(3)、公式法

算法分析:
这种方法在实际上不能实现,浮点数包含在内,取整将得不到正确答案;
(4)、平方递归算法
矩阵相乘法:

证明:

算法分析:
时间复杂度为:O(logn);
4、NxN矩阵乘法,具体描述为(矩阵乘法的顺序是不可以交换的):
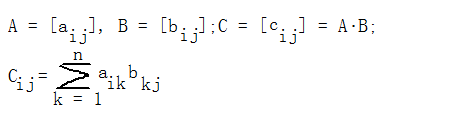
(1)、用上面的这个公式实现算法,嵌套三层for循环;
时间复杂度为:O(n^3);
(2)、矩阵分块
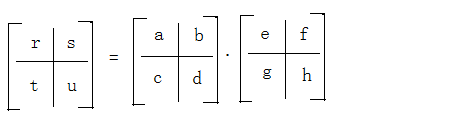
r = ae+bg、s = af+bh、t = ce+dg、u = cf+dh;
将A、B矩阵共分为a、b、c、d、e、f、g、h一共8块,在递归的计算乘积,
一共需要8次n/2乘n/2矩阵的递归乘积;
时间复杂度为:O(n^log2(8)) = O(n^3);
(3)、Strassen(斯特拉森)算法:
在上面的矩阵分块的基础上写出以下式子:
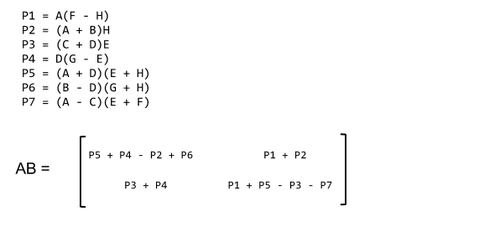
只用7次递归乘法,所有时间复杂度:O(n^log2(7)) = O(n^2.81);
矩阵相乘目前最好的算法时间复杂度大约是:O(n^2.376);
5、将完全二叉树布局到电路网格上,要求占的面积要最少(包围的树形面积)?
(1)常规的放置方案:
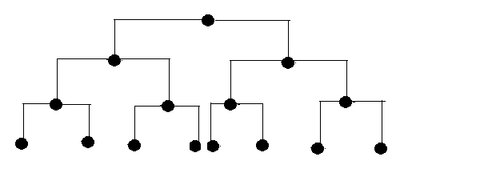
树高log(n),宽为n,所以面积为:nlog(n);
(2)、可以变换树的图形,从宽度上着手;
树的网格布局一个好方法,也是分治法思想的一个应用。
H布局
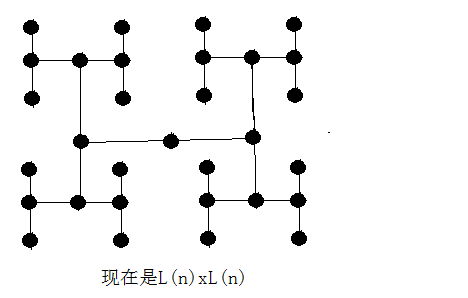
即高和宽放的都是一样多的,完全树的L(n) = O(根号n),所以面积最小为:n;
本文出自 “wait0804” 博客,请务必保留此出处http://wait0804.blog.51cto.com/11586096/1898633
分治策略
