首页 > 代码库 > Codeforces Round #267 (Div. 2) C. George and Job（DP）补题
Codeforces Round #267 (Div. 2) C. George and Job（DP）补题
Codeforces Round #267 (Div. 2) C. George and Job题目链接请点击~
The new ITone 6 has been released recently and George got really keen to buy it. Unfortunately, he didn‘t have enough money, so George was going to work as a programmer. Now he faced the following problem at the work.
Given a sequence of n integers p1, p2, ..., pn. You are to choose k pairs of integers:
in such a way that the value of sum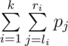 
is maximal possible. Help George to cope with the task.
Input
The first line contains three integers n, m and k (1 ≤ (m × k) ≤ n ≤ 5000). The second line contains n integersp1, p2, ..., pn (0 ≤ pi ≤ 109).
Output
Print an integer in a single line — the maximum possible value of sum.
Sample test(s)
Input
5 2 11 2 3 4 5
Output
9
Input
7 1 32 10 7 18 5 33 0
Output
61
1 #include <iostream> 2 #include <cstdio> 3 #define LL long long 4 using namespace std; 5 const int maxn = 5000 + 100; 6 LL p[maxn],s[maxn],dp[maxn][maxn]; 7 int main(){ 8 int n,m,k; 9 cin>>n>>m>>k;10 for(int i = 1;i <= n;i++){11 cin>>p[i];s[i] = s[i - 1] + p[i];12 }13 for(int i = m;i <= n;i++)14 for(int j = 1;j <= k;j++)15 dp[i][j] = max(dp[i-m][j-1]+s[i]-s[i-m],dp[i-1][j]);16 cout<<dp[n][k]<<endl;17 return 0;18 }
Codeforces Round #267 (Div. 2) C. George and Job（DP）补题
声明：以上内容来自用户投稿及互联网公开渠道收集整理发布，本网站不拥有所有权，未作人工编辑处理，也不承担相关法律责任，若内容有误或涉及侵权可进行投诉： 投诉/举报 工作人员会在5个工作日内联系你，一经查实，本站将立刻删除涉嫌侵权内容。