什么是自动机的等价性：前面我们讲过如果两个文法生成的语言相同，那么我们认为这两个文法是等价的。这里道理是一样的，如果两个自动机识别的语言相同，那么我们也认为它们是等价的。为了讨论自动机的等价性，需要先对自动机中的映射进行扩展。

1，对自动机的映射进行扩展

            原来的映射 t：Q × ∑ → Q            扩展之后的映射 t：Q × ∑* → Q

            DFA 扩展之后的映射定义为：

                        t（q，ε） = q

                        t（q，aα） = t（t（q，a），α）  其中，q ∈ Q，a ∈ ∑，α ∈ ∑*。

            NFA 扩展之后的映射定义为：

                        t（q，ε） = { q }

                        t（q，aα） = t（q1，α） ∪ t（q2，α） ∪ ... ∪ t（qn，α） 其中，a ∈ ∑，α ∈ ∑*，t（q，a） = { q1，q2，q3， ... qn }。

2，用映射的形式描述 DFA  A 是否能识别字符串 aabb

            用映射的形式描述描述自动机 A：

                        t（q0，a） = q1                        t（q0，b） = q3

                        t（q1，a） = q0                        t（q1，b） = q2

                        t（q2，a） = q3                        t（q2，b） = q1

                        t（q3，a） = q2                        t（q3，b） = q0

解：t（q0，aabb） = t（t（q0，a），abb） = t（q1，abb） = t（t（q1，a），bb） = t（q0，bb） = t（t（q0，b），b） = t（q3，b） = q0 ∈ F。即可认为 t（q0，aabb） = q0 ∈ F，所以，符号串 aabb 能被确定有穷自动机 A 所识别。并且符号串 aabb 是确定有穷自动机 A 识别符号串集 L(A) 的一个子集。 对于 DFA来说如果从开始状态出发扫描某个符号串，经过一系列的移动最后得出的状态是终止状态，那么我们认定这个符号串是能被 DFA 所识别的。

3，用映射的形式描述 NFA  A 是否能识别字符串 xyx

            用状态转换图描述描述自动机 A：

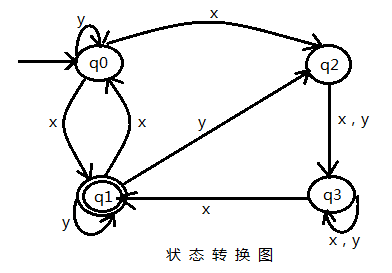
解：

            t（q0，xyx） = t（q1，yx）∪ t（q2，yx）        ### t（q0，x） = { q1，q2 }

                                  = t（q1，x）∪ t（q2，x）∪ t（q3，x）  ### t（q1，y） = { q1，q2 }，t（q2，y） = { q3 }

                                  = { q0 } ∪ { q3 } ∪ { q1，q3 }

                                  = { q0，q1，q3 }

PS：即可认为 t（q0，xyx） = { q0，q1，q3 } 。因为 q1 ∈ { q0，q1，q3 } 并且 ，q1 ∈ F 所以，符号串 xyx 能被不确定有穷自动机 A 所识别。并且符号串 xyx 是不确定有穷自动机 A 识别符号串集 L(A) 的一个子集。 对于 NFA来说如果从开始状态出发扫描某个符号串，经过一系列的移动最后得出的状态集合中包含有终止状态，那么我们认定这个符号串是能被 NFA 所识别的。

4，自动机的等价性

            两个有穷自动机 A1 和 A2，如果 L(A1) = L(A2)，则称自动机 A1 与 A2 等价。

本文出自 “珞辰的博客” 博客，谢绝转载！

自动机的等价性