首页 > 代码库 > Codeforces Round #266 (Div. 2)C. Number of Ways
Codeforces Round #266 (Div. 2)C. Number of Ways
传送门
Description
You‘ve got array a[1], a[2], ..., a[n], consisting of n integers. Count the number of ways to split all the elements of the array into three contiguous parts so that the sum of elements in each part is the same.
More formally, you need to find the number of such pairs of indices i, j (2 ≤ i ≤ j ≤ n - 1), that 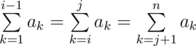 .
.
Input
The first line contains integer n (1 ≤ n ≤ 5·105), showing how many numbers are in the array. The second line contains n integers a[1], a[2], ..., a[n] (|a[i]| ≤ 109) — the elements of array a.
Output
Print a single integer — the number of ways to split the array into three parts with the same sum.
Sample Input
5
1 2 3 0 3
4
0 1 -1 0
2
4 1
Sample Output
2
1
0
思路
题意:
给定n个数,将这n个数分成连续的三组,每组数的和相同,有几种分法。
题解:
维护一个前缀和与一个后缀和,找出前缀和为 sum / 3的位置,后缀和为 sum / 3的位置,组合搭配得出结果。一个降低复杂度的技巧,记录下后缀和为 sum / 3的组数,用cnt[pos]表示pos位置开始和为sum / 3的组数,然后从头遍历的时候,当在位置pos时,前缀和为 sum / 3,则方案数有cnt[pos]种,注意:sum /3 为0时,方案数应该为 cnt[pos + 2]种。
#include<bits/stdc++.h>using namespace std;typedef __int64 LL;const int maxn = 500005;int a[maxn],cnt[maxn];int main(){ int n; LL res = 0,sum = 0; memset(cnt,0,sizeof(cnt)); scanf("%d",&n); for (int i = 0;i < n;i++) { scanf("%d",&a[i]); sum += a[i]; } if (sum % 3) { printf("0\n"); } else { sum /= 3; LL ss = 0; for (int i = n - 1;i >= 0;i--) { ss += a[i]; if (ss == sum) cnt[i]++; } for (int i = n - 2;i >= 0;i--) cnt[i] += cnt[i+1]; ss = 0; for (int i = 0;i < n - 2;i++) { ss += a[i]; if (ss == sum) res += (LL)cnt[i+2]; } printf("%I64d\n",res); } return 0;}
Codeforces Round #266 (Div. 2)C. Number of Ways
