首页 > 代码库 > poj 3735 Training little cats（矩阵构造，快速幂）

poj 3735 Training little cats（矩阵构造，快速幂）

2024-07-29 12:32:01   219人阅读

Training little cats
Time Limit: 2000MS Memory Limit: 65536K
Total Submissions: 10350 Accepted: 2471

Description

Facer‘s pet cat just gave birth to a brood of little cats. Having considered the health of those lovely cats, Facer decides to make the cats to do some exercises. Facer has well designed a set of moves for his cats. He is now asking you to supervise the cats to do his exercises. Facer‘s great exercise for cats contains three different moves:
g i : Let the ith cat take a peanut.
e i : Let the ith cat eat all peanuts it have.
s i j : Let the ith cat and jth cat exchange their peanuts.
All the cats perform a sequence of these moves and must repeat it m times! Poor cats! Only Facer can come up with such embarrassing idea. 
You have to determine the final number of peanuts each cat have, and directly give them the exact quantity in order to save them.

Input

The input file consists of multiple test cases, ending with three zeroes "0 0 0". For each test case, three integers n, m and k are given firstly, where n is the number of cats and k is the length of the move sequence. The following k lines describe the sequence.
(m≤1,000,000,000, n≤100, k≤100)

Output

For each test case, output n numbers in a single line, representing the numbers of peanuts the cats have.

Sample Input

3 1 6
g 1
g 2
g 2
s 1 2
g 3
e 2
0 0 0

Sample Output

2 0 1


k个命令执行m次，求最后每个猫的花生数。

构造矩阵：http://blog.csdn.net/magicnumber/article/details/6217602


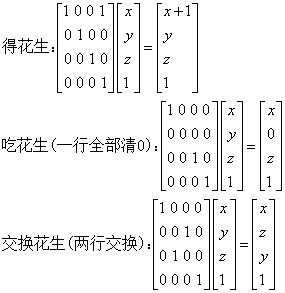
构造的是(n+1)*(n+1)矩阵，最后一列存的猫的花生数，然后矩阵快速幂，加个稀疏矩阵的优化：注意，ans.ma[i]

[k]=(ans.ma[i][k]+x.ma[i][j]*y.ma[j][k]);才可以优化，ans.ma[i][j]=(ans.ma[i][j]+x.ma[i][k]*y.ma[k][j])的不可以优

化，在这个点坑了好久。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
struct matrix
{
    long long ma[130][130];
}a;

int n,t;
long long m;
matrix multi(matrix x,matrix y)//矩阵相乘
{
    matrix ans;
    memset(ans.ma,0,sizeof(ans.ma));
    for(int i=1;i<=n+1;i++)
    {
        for(int j=1;j<=n+1;j++)
        {
            if(x.ma[i][j])//稀疏矩阵优化
            for(int k=1;k<=n+1;k++)
            {
                ans.ma[i][k]=(ans.ma[i][k]+x.ma[i][j]*y.ma[j][k]);
            }
        }
    }
    return ans;
}
int main()
{
    while(~scanf("%d%I64d%d",&n,&m,&t)&&(n+m+t))
    {
        for(int i=1;i<=n+1;i++)
        {
            for(int j=1;j<=n+1;j++)
            {
                if(i==j)
                a.ma[i][j]=1;
                else
                a.ma[i][j]=0;
            }
        }
        char s[10];
        int x,y;
        for(int i=0;i<t;i++)
        {
            scanf("%s",s);
            if(s[0]=='g')
            {
                scanf("%d",&x);
                a.ma[x][n+1]++;
            }
            if(s[0]=='e')
            {
                scanf("%d",&x);
                for(int j=1;j<=n+1;j++)
                {
                    a.ma[x][j]=0;
                }
            }
            if(s[0]=='s')
            {
                scanf("%d%d",&x,&y);
                for(int j=1;j<=n+1;j++)
                {
                    long long temp=a.ma[x][j];
                    a.ma[x][j]=a.ma[y][j];
                    a.ma[y][j]=temp;
                }
            }
        }
        matrix ans;
        for(int i=1;i<=n+1;i++)//单位矩阵
        {
            for(int j=1;j<=n+1;j++)
            {
                if(i==j)
                ans.ma[i][j]=1;
                else
                ans.ma[i][j]=0;
            }
        }
        while(m)//矩阵快速幂
        {
            if(m&1)
            {
                ans=multi(ans,a);
            }
            a=multi(a,a);
            m=(m>>1);
        }
        for(int i=1;i<=n;i++)
        printf("%I64d ",ans.ma[i][n+1]);
        printf("\n");
    }
    return 0;
}




poj 3735 Training little cats（矩阵构造，快速幂）


联系
我们