首页 > 代码库 > HDU 1159 Common Subsequence 动态规划

HDU 1159 Common Subsequence 动态规划

2024-11-19 08:56:39   205人阅读

2017-08-06 15:41:04

writer：pprp

刚开始学dp，集训的讲的很难，但是还是得自己看，从简单到难，慢慢来（如果哪里有错误欢迎各位大佬指正）

题意如下：

给两个字符串，找到其中大的公共子序列，每个样例输出一个数；

最长公共子串（Longest Common Substirng）和最长公共子序列（Longest Common Subsequence，LCS）的区别为：

　　子串是串的一个连续的部分，子序列则是从不改变序列的顺序，而从序列中去掉任意的元素而获得新的序列；

　　也就是说，子串中字符的位置必须是连续的，子序列则可以不必连续。

动态规划的思想：abcfbc 和 abfcab找匹配值（图是大佬画的，借用一下^_^）

　　
技术分享

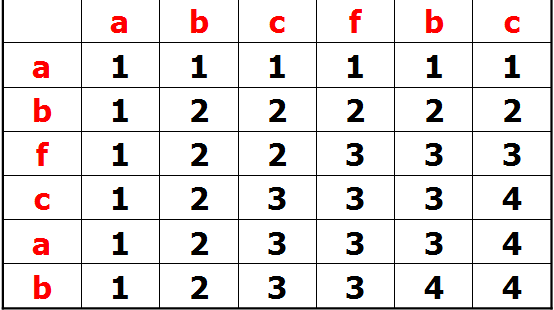
可以看出：

状态的定义：

　　当前匹配到某一位置时已经匹配的数目

状态转移：设记录匹配状态的二维数组叫a[1001][1001]

　　　　如果str1[i] == str2[j] 那么a[i][i] = a[i-1][j-1] + 1;

　　　　如果str1[i] != str2[j] 那么a[i][j] = max(a[i-1][j], a[i][j-1]);

状态结束：

　　　　匹配完成

 

代码如下：

　　

#include <iostream>
#include <string>
#include <cstring>

using namespace std;

int a[1001][1001];

int _max(int a, int b)
{
      return a > b ? a : b;
}

int main()
{
    string str1,str2;
    while(cin >> str1 >> str2)
    {
        int len1 = str1.length();
        int len2 = str2.length();

        memset(a,0,sizeof(a));

        for(int i = 1 ; i <= len1 ; i++)
        {
            for(int j = 1 ; j <= len2 ; j++)
            {
                if(str1[i-1] == str2[j-1])
                {
                    a[i][j] = a[i-1][j-1] + 1;
                }
                else
                {
                    a[i][j] = _max(a[i-1][j],a[i][j-1]);
                }
            }
        }

        cout << a[len1][len2] << endl;
    }
    return 0;
}

提交状态：ac

HDU 1159 Common Subsequence 动态规划


联系
我们