SIFT尺度不变特征

D. Lowe. Distinctive image features from scale-invariant key points, IJCV 2004

-Lecture 05 - Scale-invariant Feature Transform (SIFT)

- https://www.youtube.com/watch?v=NPcMS49V5hg

    本文是上面UCF-CRCV课程视频的学习笔记。

DOG(Difference of Gaussian)角点 / Harris point(角点) 通过z轴旋转 点位置与未旋转的点 位置重合

所以角点Harris Point具有旋转不变性

Invariance to image scale and rotation

SIFT cares Local features

Steps for Extracting Key Points

1 Scale space peak selection

        Potential locations for finding features

2 Key point localization

        Accurately locating the feature key points

3 Orientation Assignment

        Assigning orientation to the key points

4 Key point descriptor(SIFT descriptor)

        Describing the key point as a high dimensional vector

        detector VS descriptor

Scales

sigma for Canny and LG edge detection?

用来做高斯平滑的sigma如何选择。mask 的 width

zero-crossing检测出来边缘点（角点），zero-cross就是二阶导数为0的点。

Scale space(尺度空间)（Witkin, IJCAI 1983）

每一个弧形弯度定点都是一个zero-crossing

小的点会被更大scale的点包围并且替代

总结：实施全光谱尺寸的扫表，然后画出具有包含关系的zero-crossing如上图。

理解尺寸空间曲线（拱形曲线，bottom开口，顶部闭合；建立区间树）。

介绍：

尺度空间的生成目的是模拟图像数据多尺度特征。高斯卷积核是实现尺度变化的唯一线性核。

对计算机视觉而言，无法预知某种尺度的物体结构是有意的，因此有必要将所有尺度的结构表示出来。

比如温度曲线的采集，不能是无限的，这里在一定温度范围进行量化采集，温度范围即是选择的尺度。

多尺度表示方法：空间金字塔

Laplacian-of-Gaussian(LoG)

通过 LoG平滑，得到多scale的图片空间。

如何确定该点是interest point(或者说是角点)：

    取得当前尺度该点p 的9个neighbors和上下两种尺度的各9各neighbors，如果p的尺度是27各点中的最大值或者最小值点，那么p是Interest point。最后得到了(x, y, sigma)代表该点。

Approximation of LoG by Difference of Gaussians

    (k*sigm) a Gasussian filter ~~~ LoG  是通过热传导方程推导的（Heat Equation）

typically, sigma = 1.6    k = sqrt(2);

Building  a Scale Space

高斯卷积核是实现尺度变换的唯一线性核，于是一副二维图像的尺度空间定义为：

其中 G(x,y,σ) 是尺度可变高斯函数 ;（x，y）是空间坐标，是尺度坐标。σ大小决定图像的平滑程度，大尺度对应图像的概貌特征，小尺度对应图像的细节特征。大的σ值对应粗糙尺度(低分辨率)，反之，对应精细尺度(高分辨率)。为了有效的在尺度空间检测到稳定的关键点，提出了高斯差分尺度空间（DOG scale-space）。利用不同尺度的高斯差分核与图像卷积生成。

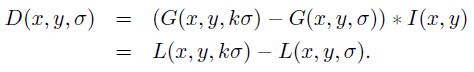
关于octave（八度）是为了实现高斯差分尺度空间，利用不同尺度的高斯差分核与图像卷积生成。每一个octave的输入都是上一层octave降采样的输出，这里因为采样的时候x , y都各减小一半，整个图像降采样之后就变为原来的1/4.

其实就是为了让每一个octave的变化差异更大，而进行认为的划分。

通过实验曲线表明 

每一个octave 中有3个scale 最好。

sigma = 1.6

去掉一系列离群点的方法

Orientation Assignment

为了实现旋转不变性，计算key point（x, y）的中央导数，梯度级，L（smooth image）的方向

 

方向上将360度分为36个bin。统计每一个key point 的邻居的方向梯度。

 

梯度和边缘是更加稳定的feature 相比较于 raw intensity values

Descriptor是描述特征的重要工具

 

上图左（并不是全部neighbors，是全部neighbors的 1/2），image中有key point找到16*16 neighbors

16 * 16 / 4 * 4 (blocks) = 16 (histograms)

each 4 * 4 = 16 blocks using 1 histogram

16 (histograms) * 8(demensions)  = 128 (demensions)  -> vector -> Sift-descriptor

然后又是实验表明：

4 x 4 blocks && 8 bins 最好

Key Point matching

foreach (d1 in A_Descriptors)

    foreach (d2 in B_Descriptors)

        find_minimum_Euclidean_distance_beteween(d1, d2);

0.1   0.15...  very close    best match 0.1 / second match 0.15 = ratio = 80%

if ratio low, first match looks good

if high,     could be ambiguous match

ratio 用来衡量第一近和第二近的两个点之间的相近程度，如果接近80% 那么干脆两个点都不选。因为有两个matching你不知道哪一个才是最好的！

Ratio 可以对correct matching  num 产生影响

 

最后

pagerank 和 论文cities的统计思想类似。 考察论文被人引用的次数，类似统计网站被别的网站链接的次数。

H index = 5  means 你已经写了至少5篇papers，这些文章至少被引用了5次。

【学习笔记】SIFT尺度不变特征 （配合UCF-CRCV课程视频）