首页 > 代码库 > 10分钟入门opengl投影变换推导(内含mathjax公式)

10分钟入门opengl投影变换推导(内含mathjax公式)

2024-07-03 22:13:16   224人阅读

 

<style></style><style></style><script type="text/javascript">// /gm,">")}function b(p){for(var o=p.firstChild;o;o=o.nextSibling){if(o.nodeName=="CODE"){return o}if(!(o.nodeType==3&&o.nodeValue.match(/\s+/))){break}}}function h(p,o){return Array.prototype.map.call(p.childNodes,function(q){if(q.nodeType==3){return o?q.nodeValue.replace(/\n/g,""):q.nodeValue}if(q.nodeName=="BR"){return"\n"}return h(q,o)}).join("")}function a(q){var p=(q.className+" "+q.parentNode.className).split(/\s+/);p=p.map(function(r){return r.replace(/^language-/,"")});for(var o=0;o"}while(x.length||v.length){var u=t().splice(0,1)[0];y+=l(w.substr(p,u.offset-p));p=u.offset;if(u.event=="start"){y+=s(u.node);r.push(u.node)}else{if(u.event=="stop"){var o,q=r.length;do{q--;o=r[q];y+=("")}while(o!=u.node);r.splice(q,1);while(q‘+L[0]+""}else{r+=L[0]}N=A.lR.lastIndex;L=A.lR.exec(K)}return r+K.substr(N)}function z(){if(A.sL&&!e[A.sL]){return l(w)}var r=A.sL?d(A.sL,w):g(w);if(A.r>0){v+=r.keyword_count;B+=r.r}return‘‘+r.value+""}function J(){return A.sL!==undefined?z():G()}function I(L,r){var K=L.cN?‘‘:"";if(L.rB){x+=K;w=""}else{if(L.eB){x+=l(r)+K;w=""}else{x+=K;w=r}}A=Object.create(L,{parent:{value:A}});B+=L.r}function C(K,r){w+=K;if(r===undefined){x+=J();return 0}var L=o(r,A);if(L){x+=J();I(L,r);return L.rB?0:r.length}var M=s(A,r);if(M){if(!(M.rE||M.eE)){w+=r}x+=J();do{if(A.cN){x+=""}A=A.parent}while(A!=M.parent);if(M.eE){x+=l(r)}w="";if(M.starts){I(M.starts,"")}return M.rE?0:r.length}if(t(r,A)){throw"Illegal"}w+=r;return r.length||1}var F=e[D];f(F);var A=F;var w="";var B=0;var v=0;var x="";try{var u,q,p=0;while(true){A.t.lastIndex=p;u=A.t.exec(E);if(!u){break}q=C(E.substr(p,u.index-p),u[0]);p=u.index+q}C(E.substr(p));return{r:B,keyword_count:v,value:x,language:D}}catch(H){if(H=="Illegal"){return{r:0,keyword_count:0,value:l(E)}}else{throw H}}}function g(s){var o={keyword_count:0,r:0,value:l(s)};var q=o;for(var p in e){if(!e.hasOwnProperty(p)){continue}var r=d(p,s);r.language=p;if(r.keyword_count+r.r>q.keyword_count+q.r){q=r}if(r.keyword_count+r.r>o.keyword_count+o.r){q=o;o=r}}if(q.language){o.second_best=q}return o}function i(q,p,o){if(p){q=q.replace(/^((",r:10},{cN:"tag",b:"<style(?=\\s|>|$)",e:">",k:{title:"style"},c:[b],starts:{e:"</style>",rE:true,sL:"css"}},{cN:"tag",b:"<script(?=\\s|>|$)",e:">",k:{title:"script"},c:[b],starts:{e:"<\/script>",rE:true,sL:"javascript"}},{b:"",sL:"vbscript"},{cN:"tag",b:"",c:[{cN:"title",b:"[^ />]+"},b]}]}}(hljs);hljs.LANGUAGES.http=function(a){return{i:"\\S",c:[{cN:"status",b:"^HTTP/[0-9\\.]+",e:"$",c:[{cN:"number",b:"\\b\\d{3}\\b"}]},{cN:"request",b:"^[A-Z]+ (.*?) HTTP/[0-9\\.]+$",rB:true,e:"$",c:[{cN:"string",b:" ",e:" ",eB:true,eE:true}]},{cN:"attribute",b:"^\\w",e:": ",eE:true,i:"\\n|\\s|=",starts:{cN:"string",e:"$"}},{b:"\\n\\n",starts:{sL:"",eW:true}}]}}(hljs);hljs.LANGUAGES.java=function(a){return{k:"false synchronized int abstract float private char boolean static null if const for true while long throw strictfp finally protected import native final return void enum else break transient new catch instanceof byte super volatile case assert short package default double public try this switch continue throws",c:[{cN:"javadoc",b:"/\\*\\*",e:"\\*/",c:[{cN:"javadoctag",b:"@[A-Za-z]+"}],r:10},a.CLCM,a.CBLCLM,a.ASM,a.QSM,{cN:"class",bWK:true,e:"{",k:"class interface",i:":",c:[{bWK:true,k:"extends implements",r:10},{cN:"title",b:a.UIR}]},a.CNM,{cN:"annotation",b:"@[A-Za-z]+"}]}}(hljs);hljs.LANGUAGES.php=function(a){var e={cN:"variable",b:"\\$+[a-zA-Z_\x7f-\xff][a-zA-Z0-9_\x7f-\xff]*"};var b=[a.inherit(a.ASM,{i:null}),a.inherit(a.QSM,{i:null}),{cN:"string",b:‘b"‘,e:‘"‘,c:[a.BE]},{cN:"string",b:"b‘",e:"‘",c:[a.BE]}];var c=[a.BNM,a.CNM];var d={cN:"title",b:a.UIR};return{cI:true,k:"and include_once list abstract global private echo interface as static endswitch array null if endwhile or const for endforeach self var while isset public protected exit foreach throw elseif include __FILE__ empty require_once do xor return implements parent clone use __CLASS__ __LINE__ else break print eval new catch __METHOD__ case exception php_user_filter default die require __FUNCTION__ enddeclare final try this switch continue endfor endif declare unset true false namespace trait goto instanceof insteadof __DIR__ __NAMESPACE__ __halt_compiler",c:[a.CLCM,a.HCM,{cN:"comment",b:"/\\*",e:"\\*/",c:[{cN:"phpdoc",b:"\\s@[A-Za-z]+"}]},{cN:"comment",eB:true,b:"__halt_compiler.+?;",eW:true},{cN:"string",b:"<<</script><script type="text/javascript">// </script><script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script><script type="text/javascript">// </script>

perspective projection

title: perspective projection tags: ["openGL", "Markdown", "mathjax"] notebook: notes

关于投影变换

NDC

我们先介绍一个概念,NDC(Normalized Device Coordinates).我们在opengl右手坐标系里建立的模型都会映射到NDC.所以所有的点坐标的分量都会在[-1,1]间,超出的将被clip掉.尔后,NDC将坐标映射到viewport(视口),那为什么会有NDC这个中间产物?计算方便.不管是在后面映射视口,还是矩阵计算.特别要注意的是NDC是左手坐标系

ndc

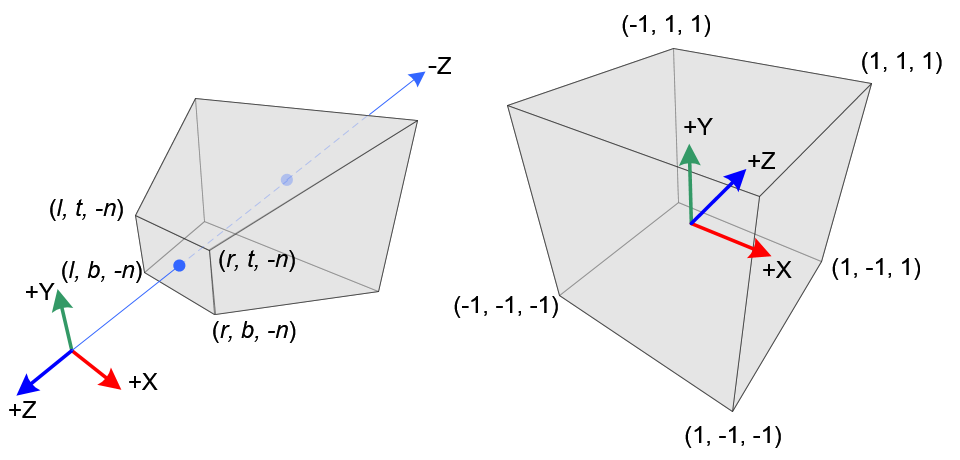
ndc 左为perspective projection,这跟我们看到的真实世界是一样的原理.有很强的3D视感.而右边.则是ortho projection,如果你学过工程制图.想必也很熟悉.没有近大远小的概念 下面,我们试着计算投影公式.这里我们用一下缩写

\cases{l=left \\ r=right \\ f=far \\ n=near \\ b=bottom \\ t=top}

<script id="MathJax-Element-1" type="math/tex; mode=display"> \cases{l=left \\ r=right \\ f=far \\ n=near \\ b=bottom \\ t=top} </script>

将下图的立方体空间映射到NDC空间.假设下面空间中一点(x,y,z,w)<script id="MathJax-Element-2" type="math/tex">(x,y,z,w)</script>,求(x_{ndc},y_{ndc},z_{ndc},w_{ndc})<script id="MathJax-Element-3" type="math/tex">(x_{ndc},y_{ndc},z_{ndc},w_{ndc})</script>

\frac{r-l}{2}=\frac{x-l}{x_{ndc}+1} => x_{ndc}=\frac{2}{r-l}x+\frac{l+r}{l-r}\

<script id="MathJax-Element-4" type="math/tex; mode=display"> \frac{r-l}{2}=\frac{x-l}{x_{ndc}+1} => x_{ndc}=\frac{2}{r-l}x+\frac{l+r}{l-r}\ </script>

y_{ndc},z_{ndc}<script id="MathJax-Element-5" type="math/tex">y_{ndc},z_{ndc}</script>同理,很容易得到矩阵 \left[ \begin{array}{cccccccccccccc} \frac{2}{r-l}&0&0& \frac{l+r}{l-r} \\ 0&\frac{2}{t-b}&0& \frac{b+t}{b-t} \\ 0&0&\frac{2}{f-n}& \frac{n+f}{n-f} \\ 0&0&0&1 \\ \end{array} \right]

<script id="MathJax-Element-6" type="math/tex; mode=display"> \left[ \begin{array}{cccccccccccccc} \frac{2}{r-l}&0&0& \frac{l+r}{l-r} \\ 0&\frac{2}{t-b}&0& \frac{b+t}{b-t} \\ 0&0&\frac{2}{f-n}& \frac{n+f}{n-f} \\ 0&0&0&1 \\ \end{array} \right] </script>

frustum 1

 

同样,根据等比公式,得到如下公式,我们假设还一组中间变量(x_{p},y_{p},z_{p},w_{p})<script id="MathJax-Element-7" type="math/tex">(x_{p},y_{p},z_{p},w_{p})</script>,代表(x,y,z,w)<script id="MathJax-Element-8" type="math/tex">(x,y,z,w)</script>映射到near面上的点.(注意,这里还没有转换到NDC) \cases{\frac{z}{x}=\frac{-n}{x_p}\\ \frac{z}{y}=\frac{-n}{y_p}\\ z_p=n} => \cases{x_p=\frac{-nx}{z} \\ y_p=\frac{-ny}{z} \\ z_p=n}

<script id="MathJax-Element-9" type="math/tex; mode=display"> \cases{\frac{z}{x}=\frac{-n}{x_p}\\ \frac{z}{y}=\frac{-n}{y_p}\\ z_p=n} => \cases{x_p=\frac{-nx}{z} \\ y_p=\frac{-ny}{z} \\ z_p=n} </script> 到这,我们已经做完了投影影射90%的工作,接下来我们需要将投影点再映射到NDC

以x_p<script id="MathJax-Element-10" type="math/tex">x_p</script>为例 \cases{al+b=-1\\ ar+b=1} => \cases{a=\frac{2}{r-l}\\ b=\frac{l+r}{l-r}}

<script id="MathJax-Element-11" type="math/tex; mode=display"> \cases{al+b=-1\\ ar+b=1} => \cases{a=\frac{2}{r-l}\\ b=\frac{l+r}{l-r}} </script> 也就是说 x_p<script id="MathJax-Element-12" type="math/tex">x_p</script> 在NDC里的映射是用这个线性函数

x_{ndc}=\frac{2}{r-l}x_p+\frac{l+r}{l-r}=\frac{2}{r-l}\frac{-nx}{z}+\frac{l+r}{l-r}

<script id="MathJax-Element-13" type="math/tex; mode=display"> x_{ndc}=\frac{2}{r-l}x_p+\frac{l+r}{l-r}=\frac{2}{r-l}\frac{-nx}{z}+\frac{l+r}{l-r} </script> 我们发现个问题..这写不过矩阵.但又发现,左右乘以z,有一些新发现

z_{x_{ndc}}=\frac{-2n}{r-l}_x + \frac{l+r}{l-r} z

<script id="MathJax-Element-14" type="math/tex; mode=display"> z_{x_{ndc}}=\frac{-2n}{r-l}_x + \frac{l+r}{l-r} z </script>

是不是有点感觉了

\left[ \begin{array}{cccccccccccccc} \frac{-2n}{r-l}&0&\frac{l+r}{l-r}&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ \end{array} \right]\left[ \begin{array}{cccccccccccccc} x\\ 0\\ 0\\ 1\\ \end{array} \right] =\left[ \begin{array}{cccccccccccccc} {x_{ndc}}*z\\ 0\\ 0\\ 0\\ \end{array} \right]\

<script id="MathJax-Element-15" type="math/tex; mode=display"> \left[ \begin{array}{cccccccccccccc} \frac{-2n}{r-l}&0&\frac{l+r}{l-r}&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ \end{array} \right]\left[ \begin{array}{cccccccccccccc} x\\ 0\\ 0\\ 1\\ \end{array} \right] =\left[ \begin{array}{cccccccccccccc} {x_{ndc}}*z\\ 0\\ 0\\ 0\\ \end{array} \right]\ </script>

同理,得到y_p<script id="MathJax-Element-16" type="math/tex">y_p</script>

\left[ \begin{array}{cccccccccccccc} \frac{-2n}{r-l}&0&\frac{l+r}{l-r}&0\\ 0&\frac{-2b}{t-b}&\frac{b+t}{b-t}&0\\ 0&0&0&0\\ 0&0&0&0\\ \end{array} \right]\left[ \begin{array}{cccccccccccccc} x\\ y\\ 0\\ 1\\ \end{array} \right]=\left[ \begin{array}{cccccccccccccc} x_{ndc} * z\\ y_{ndc}*z\\ 0\\ 0\\ \end{array} \right]\

<script id="MathJax-Element-17" type="math/tex; mode=display"> \left[ \begin{array}{cccccccccccccc} \frac{-2n}{r-l}&0&\frac{l+r}{l-r}&0\\ 0&\frac{-2b}{t-b}&\frac{b+t}{b-t}&0\\ 0&0&0&0\\ 0&0&0&0\\ \end{array} \right]\left[ \begin{array}{cccccccccccccc} x\\ y\\ 0\\ 1\\ \end{array} \right]=\left[ \begin{array}{cccccccccccccc} x_{ndc} * z\\ y_{ndc}*z\\ 0\\ 0\\ \end{array} \right]\ </script>

到这个地方我得停住说点别的. 上面公式中,我们求到的点都是放大了当前点的z倍. 所以必须除以z.而除z这个操作,学名叫 perspective divide,这个操作不用你操心,opengl 管线中会自动处理.自动除z??不对啊.我们在投影变换完后z_{npc}<script id="MathJax-Element-18" type="math/tex">z_{npc}</script>轴都在一个平面了.还原不出原始的z了啊! 人类的智慧是无穷的.我们可以将z复制到在w分量上,所以管线中的perspective divide操作其实就是除以w.而w=z.这样我们就得到矩阵第4行的值.要还原投影点,perspective divide将(x_p,y_p,z_p)<script id="MathJax-Element-19" type="math/tex">(x_p,y_p,z_p)</script>分别除以z(z=w).得到的点为(x_p/z,y_p/z,z_p/z,z)<script id="MathJax-Element-20" type="math/tex">(x_p/z,y_p/z,z_p/z,z)</script>, 请特别注意它们的下标!!要除的z是最原始点的z. 我们尝试构造第三行.

A,B,C,D

<script id="MathJax-Element-21" type="math/tex; mode=display">A,B,C,D</script>

\left[ \begin{array}{cccccccccccccc} \frac{-2n}{r-l}&0&\frac{l+r}{l-r}&0\\ 0&\frac{-2b}{t-b}&\frac{b+t}{b-t}&0\\ A&B&C&D\\ 0&0&1&0\\ \end{array} \right]\left[ \begin{array}{cccccccccccccc} x\\ y\\ z\\ 1\\ \end{array} \right]=\left[ \begin{array}{cccccccccccccc} x_{ndc_z} \\ y_{ndc_z}\\ z\\ z\\ \end{array} \right]\

<script id="MathJax-Element-22" type="math/tex; mode=display"> \left[ \begin{array}{cccccccccccccc} \frac{-2n}{r-l}&0&\frac{l+r}{l-r}&0\\ 0&\frac{-2b}{t-b}&\frac{b+t}{b-t}&0\\ A&B&C&D\\ 0&0&1&0\\ \end{array} \right]\left[ \begin{array}{cccccccccccccc} x\\ y\\ z\\ 1\\ \end{array} \right]=\left[ \begin{array}{cccccccccccccc} x_{ndc_z} \\ y_{ndc_z}\\ z\\ z\\ \end{array} \right]\ </script>

$$

Ax+By+Cz+D=z_{ndc}*z

<script id="MathJax-Element-23" type="math/tex; mode=display"> Ax+By+Cz+D=z_{ndc}*z </script> 我们知道这个方程组,有两个解(要注意z值是在动态变化的)

\cases{ Ax+By+Cn+D=-1_n \\ Ax+By+Cf+D= 1_f }

<script id="MathJax-Element-24" type="math/tex; mode=display"> \cases{ Ax+By+Cn+D=-1_n \\ Ax+By+Cf+D= 1_f } </script> 不妨令A=B=0<script id="MathJax-Element-25" type="math/tex">A=B=0</script>,使其与x,y<script id="MathJax-Element-26" type="math/tex">x,y</script>无关,解以下方程组 \cases{ Cn+D=-n \ Cf+D=f }=>\cases{C=\frac{f+n}{f-n}\\ D=\frac{2fn}{f-n}}
<script id="MathJax-Element-27" type="math/tex; mode=display"> \cases{ Cn+D=-n \ Cf+D=f }=>\cases{C=\frac{f+n}{f-n}\\ D=\frac{2fn}{f-n}} </script> 到此,我们求得投影变化矩阵为

\left[ \begin{array}{cccccccccccccc} \frac{-2n}{r-l}&0&\frac{l+r}{l-r}&0\\ 0&\frac{-2b}{t-b}&\frac{b+t}{b-t}&0\\ 0&0&\frac{f+n}{f-n}&\frac{2fn}{f-n}\\ 0&0&1&0\\ \end{array} \right]

<script id="MathJax-Element-28" type="math/tex; mode=display"> \left[ \begin{array}{cccccccccccccc} \frac{-2n}{r-l}&0&\frac{l+r}{l-r}&0\\ 0&\frac{-2b}{t-b}&\frac{b+t}{b-t}&0\\ 0&0&\frac{f+n}{f-n}&\frac{2fn}{f-n}\\ 0&0&1&0\\ \end{array} \right] </script>

frustum 2

frustum 1 介绍的方法,需要6参数.而且不太直观.下面介绍另一种常见的构造投影变换的方法. 不管用什么方法,只要参数能够确定唯一的一个frustum.就行. 我们先看一张网上淘来的图..

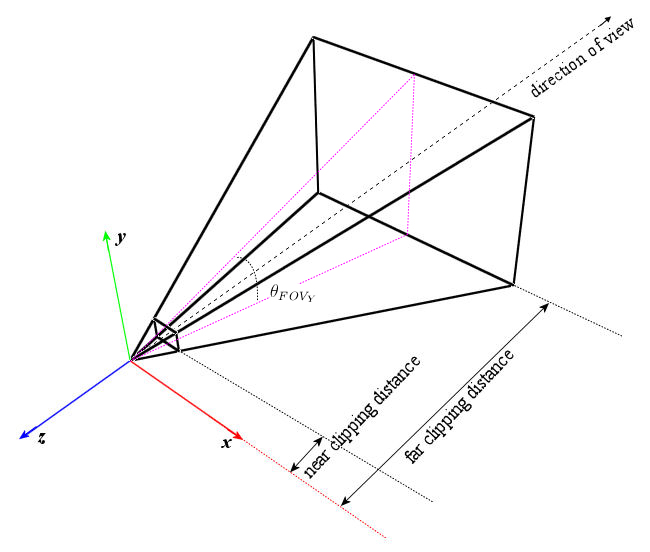
frustum 2

fov=field of view.视野,我们假定它为相机上平面与下平面的夹角\theta<script id="MathJax-Element-29" type="math/tex">\theta</script>.

near,跟 far 就很显然了. 我们还需要一个参数.那就是近平面的宽高比值记作ar(aspect ratio).

好了.参数有了. \theta<script id="MathJax-Element-30" type="math/tex">\theta</script>,ar,n,f, 下面求矩阵 因为z_{ndc}<script id="MathJax-Element-31" type="math/tex">z_{ndc}</script>的投影变换只与n,f有关,上面frustum 1中已经有公式.不再赘述. 比如先求y_{ndc}<script id="MathJax-Element-32" type="math/tex">y_{ndc}</script>,我们垂直从+x看到-x.很容易得到如下公式 \frac{y_p}{n}=\frac{y}{z} => y_p=\frac{y}{z}\dot{}n

<script id="MathJax-Element-33" type="math/tex; mode=display"> \frac{y_p}{n}=\frac{y}{z} => y_p=\frac{y}{z}\dot{}n </script> 再将y映射到y_{ndc}<script id="MathJax-Element-34" type="math/tex">y_{ndc}</script>: \frac{y_{ndc}-(-1)}{2}=\frac{y_p-b}{tan\theta\dot{}n}
<script id="MathJax-Element-35" type="math/tex; mode=display"> \frac{y_{ndc}-(-1)}{2}=\frac{y_p-b}{tan\theta\dot{}n} </script> 而其中 b=-tan\frac{\theta}{2}\dot{}n
<script id="MathJax-Element-36" type="math/tex; mode=display"> b=-tan\frac{\theta}{2}\dot{}n </script> 解方程得到: y_{ndc}\dot{}z=\frac{y}{tan\frac{\theta}{2}}
<script id="MathJax-Element-37" type="math/tex; mode=display"> y_{ndc}\dot{}z=\frac{y}{tan\frac{\theta}{2}} </script> 同理得到 x_{ndc}\dot{}z=\frac{x}{ar\dot{}tan\frac{\theta}{2}}
<script id="MathJax-Element-38" type="math/tex; mode=display"> x_{ndc}\dot{}z=\frac{x}{ar\dot{}tan\frac{\theta}{2}} </script> 后面的计算frustum 1里已经说过.组合一下上面的结果为:

\left[ \begin{array}{cccccccccccccc} \frac{1}{ar\dot{}tan\frac{\theta}{2}}&0&0&0\\ 0&\frac{1}{tan\frac{\theta}{2}}&0&0\\ 0&0&\frac{f+n}{f-n}&\frac{2fn}{f-n}\\ 0&0&1&0\\ \end{array} \right]

<script id="MathJax-Element-39" type="math/tex; mode=display"> \left[ \begin{array}{cccccccccccccc} \frac{1}{ar\dot{}tan\frac{\theta}{2}}&0&0&0\\ 0&\frac{1}{tan\frac{\theta}{2}}&0&0\\ 0&0&\frac{f+n}{f-n}&\frac{2fn}{f-n}\\ 0&0&1&0\\ \end{array} \right] </script>


联系
我们