Description

Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d. 

We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates. 
 
Figure A Sample Input of Radar Installations

Input

Output

Sample Input

3 2
1 2
-3 1
2 1

1 2
0 2

0 0

Sample Output

Case 1: 2
Case 2: 1

Source

题意为，在一个坐标系中，x中代表海岸，x轴以上有n个点，代表着n个岛屿，在x轴上建雷达，一直雷达的覆盖范围为半径为d的圆，求在x轴上最少建多少个雷达，才能把全部的岛屿覆盖起来，如果不能覆盖，输出-1.

区间选点问题为  给定 n个闭区间,求在里面选择最少的点使得每个区间里面都包含至少一个点（一个点可以在不同的区间)。   比如下图。

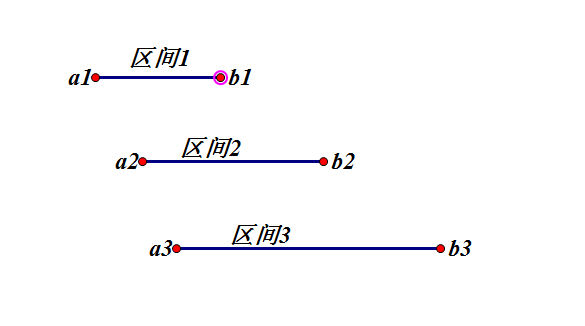
贪心策略为  把n个区间先按照右端点从小到大进行排序，如果端点相同，按照左端点从大到小进行排序。首先选择第一个区间的右端点。如果以后的区间左端点大于当前选择的端点值时，使得当前选择的端点值改变为这个以后的区间的右端点值。 比如 当前temp是 23  遇到一个区间左端点 25 右端点 27，让temp=27.（选择了一个新点）

回到本题上来，要求建造最短的雷达。  首先对n个岛屿进行画圆，与x轴有两个交点，这样每个岛屿都对应了一个区间（只要雷达建在这个区间内，该岛屿就一定能被覆盖到）。圆的方程(x－a)2+(y－b)2=r2 ,在本题中，b始终是0，因为在x轴上。判断无解的条件为r<y 。我们得到了n个区间，这样问题也就转化为了在这n个区间里面选择尽可能少的点，使得这n个区间中每个区间都至少有一个点。 按照上面的方法做就可以了。

参考：

http://blog.csdn.net/dgq8211/article/details/7534776

代码：

#include <iostream>
#include <string.h>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn=1010;

struct N
{
    double l,r;
}interval[maxn];

bool cmp(N a,N b)//排序
{
    if(a.r<b.r)
        return true;
    else if(a.r==b.r)
    {
        if(a.l>b.l)
            return true;
        return false;
    }
    return false;
}


int main()
{
    double x,y;
    int n,d;
    int c=1;
    while(cin>>n>>d&&(n||d))
    {
        bool ok=1;
        for(int i=1;i<=n;i++)
        {
            cin>>x>>y;
            double temp=d*d-y*y;
            if(temp<0||d<0)//这样的话就得判断d是否小于0,如果 temp= d-y 这样写的话，就不用判断d是否小于0，坑啊！！
                ok=0;
            else if(ok)
            {
                interval[i].l=x-sqrt((double)d*d - (double)y*y);
                interval[i].r=x+sqrt((double)d*d - (double)y*y);
            }
        }
        if(!ok)
        {
            cout<<"Case "<<c++<<": "<<-1<<endl;
            continue;
        }
        sort(interval+1,interval+1+n,cmp);
        int cnt=1;
        double temp=interval[1].r;
        for(int i=2;i<=n;i++)
        {
            if(temp<interval[i].l)
            {
                cnt++;
                temp=interval[i].r;
            }
            
        }
       /* for(int i=2;i<=n;i++)
        {
            if(interval[i].l>temp)
            {
                cnt++;
                temp=interval[i].l;
            }
        }*/   //一开始写成了这个，不对  比如区间 [1,2]  [4,8]  [6,9],正确的应该是选择2，8这两个点，而上面这个则选择了 2,4 6，显然不对
        cout<<"Case "<<c++<<": "<<cnt<<endl;
    }
    return 0;
}