1. 问题原型：

???????? 给定一篇网页，当中有非常多敏感词汇或者无效的词，须要找到一种算法，找到这些敏感词。

2. 怎样求解呢？
?? 2.1 第一个简单的思路是：
????????? step1： for i = 0 to in #text???
????????? step2:?????? foreach pattern p?
????????? step3：?????????? 比較 text[i+j] and p[0+j]? where j = 0 to #p??

???? 这个思路最大问题是，逐个比較每一个文本和每一个模式，算法的复杂度是O(m*n*k),m是文本长度，n是pattern个数，k是全部pattern的总长度。my god！可想而知，这种算法是不可容忍的。那么有哪些改进方法呢：

???? 首先, hash_map 能够降低大量的比較。

???? 其次， 对一个模式的比較，有非常多算法如: KMP和Boyer-Moore。这两个改进的算法思想是：比較过的文本就不须要在比較了,直接shift 模式而不须要回溯Text，这两个算法能够看这里。以后有机会具体讨论这些。多模式匹配算法也是能够有相似的方法。
??? 我们知道，单模式匹配算法的复杂度能够达到O(m+n)，所以最主要的改进是：
??? 2.2.? naive muti-pattern match
?????????? step1: foreach pattern p
?????????? step2:??????? 运行 O(m+#p)的单模式匹配算法?
????????? 算法复杂度是： O(m + #P1 + m + #P2 + …… + m + #pn) = O( n*m + k)

??? 好慢！假设模式的个数有几百万个，速度是不可忍受

3. 有哪些算法解决多模式匹配问题：
??? AC (Aho-Corasick algorithm)
??? ACBM(CW)[ A String Matching Algorithm Fast on the Average ]
??? WM [Wu and Manber]
??? ACQS
??? DAWG(ACRF)
??? MultiBDM

3.1 Aho-Corsick Algorithm:
AC 算法的核心思想是构造词典的自己主动机(能够使用trie树来实现)， 其算法复杂度是O(m+k+z), m是文本长度，k是全部pattern长度之和，z是字符串中出现pattern的个数。

举个样例来说：Pattern P = {he; she; his; hers} ，AC算法将建立例如以下图的字典树（或者成为keyword tree）

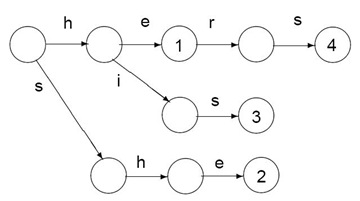
当中node中有数字的表示在词典（pattern）中，每一条边表示一个字符，同一个节点指出的不同边拥有不同的字符标签。朴素字典树的构建相当简单,?? 仅仅须要一个pattern一个pattern的插入就能够了（当然其它改进的算法和改进的数据结构，如double-trie）

Construction：
1. foreach pattern in P{p1,p2,…,pn}
2. start at the Root
??? 2.1 假设从根节点出发的路径在Pi结束之前结束，创建为Pi中每一个没有结束的字符创建节点。 否则继续搜索
??? 2.2 创建Pi的终止节点，设置唯一标识
一旦字典数构建结束，查找过程跟我们平时用查字典的过程是一样的，从根节点一步步向下查，直到找到该词或者没有之结点为止。可是，从以上过程我们发现其复杂度是O（m×k），这显然不是我们想要的结果。okay，那我们该建立一个自己主动机（automaton）：

自己主动机由状态（states）和行动（action）组成，在本例中：
State:?? 字典树的节点，初始状态为0
Action:? action有3个函数决定：
?????????? 1. goto函数 g（q,a）, 它表示，假设当前状态是q，输入输入字符是a，那么下一个状态是g(q,a)
?????????????? a)假设边edge(q, r) 标记为a， 那么 g（q,a) = r
?????????????? b) 假设a不输入0状态的出边 g（0,a)? = 0 , g(q,a) =? $(空)
?????????? 2. failure函数 f（q）， 对q不为0的状态，failure函数表示在状态q失配
?????????????? f（q）是状态机中的一个节点，标记为pattern中某个pattern恰当的最长后缀（例如以下图5的he）
?????????? 3. out函数 out（q）， 状态q，识别出某个pattern

虚线就是表示failure函数的action，比方从5到2的action。假设字符串为sher，搜索到s—h—e，下一个串是r，failure函数能够使得字典树的搜索从5，跳到2， （{he} 是{ she} 的后缀），然后迅速的找到her。 能够看到整个过程中，匹配过程直接依照自己主动机的顺序匹配，根本不须要回溯字符串（比方sher的样例，一旦she找到，直接从e的下一个字符r開始匹配，而不是从s的下一个字符h開始）。算法例如以下：

step1 q = 0
step2 for i = 0 to m do
step3????? while (g(q, T[i])) == $ do
step4??????????? q = f(q)
step5?????? q = g(q, T[i])
step6?????? if out(q) != $ then output(q)

好简洁，这个搜索过复杂度是O（m+z）z是pattern在字符串中出现的次数！证明从略^_^

问题是，这个AC自己主动机怎样构建？

1. 第一步：构建字典数，和root
2. 第二步：构建failure函数

第一步：
??????? 1.1 构建字典数， foreach pattern pi in P，设置out（v）= pi，假设v节点标记为pi
??????? 1.2 构建root， g（0,a) = 0, 假设a不是root的输出边

结果如图：

?

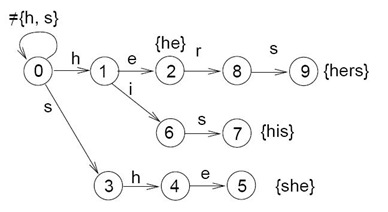第二步：
第二步基于一个简单的事实，假设 g(q,a) = u (q---a--->u), 而且{f(q),f(f(q)), f(f(f(q)))…,root}都已经计算出来,那么f(u)为
第一个不为空的g(fi(q),a)，说起来好绕口啊，还是直接看算法吧：

1.? Q = emptyQueue
2.? foreach a in alphabet??
3?????? if q(0,a) == q != 0 then
4????????????? f(q):=0; Q.enqueue(q)?
5?? while no Q.empty() do
6?????? r = Q.dequeue()
7?????? foreach a in alphabet
8?????????? if g(r,a) == u != null then
9?????????????? Q.enqueue(u)
10????????????? v = f(r)
11????????????? while g(v,a) == null do v = f(v)
12????????????? f(u) = g(v,a)
13????????????? out(u) = out(u) union out(f(u))

大功告成！注意，AC算法对多模式匹配的一些变种问题也能够非常好的处理(e.g? pattern中含有通配符，甚至是正則表達式）,代码我就不贴了，download here! ac.h, ac.c

參考：
1.? http://www.egeen.ee/u/vilo/edu/2005-06/Text_Algorithms/index.cgi?f=L2_Multiple_String
2.? http://www.itl.nist.gov/div897/sqg/dads/HTML/boyermoore.html

下一篇多模式匹配的ACBM算法，当中还涉及单个模式匹配（或者称为Exact search）的Boyer-Moore技术