城市才是要构造的二分图的顶点！

构造方法如下：

例如输入：

*oo

***

O*o

时，可以抽象为一个数字地图：

100

234

050

数字就是根据输入的城市次序作为该城市的编号，0代表该位置没有城市。

然后根据题目的“范围”规则，从第一个城市开始，以自身作为中心城市，向四个方向的城市进行连线（覆盖）

因此就能够得到边集：

e12  e21     e32     e43    e53

     e23     e34

             e35

可以看到，这些边都是有向边，但是每一条边都有与其对应的一条相反边。

即任意两个城市（顶点）之间的边是成对出现的

那么我们就可以确定下来，应该 构造无向二分图（其实无向=双向）

因为若要构造有向的二分图时，需要判断已出现的边，是很麻烦的工作

为了把有向图G构造为无向二分图，这里需要引入一个新名词“拆点”

其实就是把原有向图G的每一个顶点都”拆分（我认为复制更准确）”为2个点，分别属于所要构造的二分图的两个顶点集

例如在刚才的例子中抽出一条有向边e12举例说明：

复制顶点1和顶点2，使得1，2∈V1；  1’，2’∈V2 ，不难发现|V1|=|V2|

根据边e12和e21，得到无向二分图：

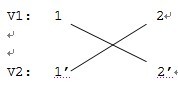
那么同理就可以得到刚才的例子的 无向二分图为：

再继而通过无向二分图，以V1的元素作为row，V2的元素作为col，构造 可达矩阵 存储到计算机

   1’  2’  3’  4’  5’

1  F  T   F   F   F

2  T  F   T   F   F

3  F  T   F   T   T

4  F  F   T   F   F

5  F  F   T   F   F

接下来就是要求这个 无向二分图的最小路径覆盖 了

利用公式：

无向二分图的最小路径覆盖 = 顶点数 – 最大二分匹配数/2

顶点数：就是用于构造无向二分图的城市数，即进行“拆点”操作前的顶点数量

最大二分匹配书之所以要除以2，是因为进行了“拆点”擦奥做做使得匹配总数多了一倍，因此除以2得到原图的真正的匹配数

最后剩下的问题就是求最大二分匹配数了，用匈牙利算法，这就不多说了，参考POJ3041的做法，基本一摸一样。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int map[45][41];
int city[405][405];
int vis[405],link[405];
int sum,v1,v2,ip;
int dx[4]={1,0,-1,0};
int dy[4]={0,-1,0,1};
int xyl(int x)
{
    int i;
    for(i=1;i<=v2;i++)
        if(city[x][i]&&!vis[i])
    {
        vis[i]=1;
        if(!link[i]||xyl(link[i]))
        {
            link[i]=x;
            return 1;
        }
    }
    return 0;
}
void search()
{
    int i;
    for(i=1;i<=v1;i++)
    {
        memset(vis,0,sizeof vis);
        if(xyl(i))
            sum++;
    }
    return ;
}
int main()
{
    int cas,i,j,row,col;
    cin>>cas;
    while(cas--)
    {
        memset(map,0,sizeof map);
        memset(city,0,sizeof city);
        memset(link,0,sizeof link);
        ip=0;
        sum=0;

        cin>>row>>col;
        char a;
        for(i=1;i<=row;i++)
            for(j=1;j<=col;j++)
            {
                cin>>a;
                if(a=='*')
                    map[i][j]=++ip;
            }
        for(i=1;i<=row;i++)
            for(j=1;j<=col;j++)
                if(map[i][j])
                for(int k=0;k<4;k++)
                {
                    int xx=i+dx[k];
                    int yy=j+dy[k];
                    if(map[xx][yy])
                        city[map[i][j]][map[xx][yy]]=1;
                }
                v1=v2=ip;
                search();
                cout<<ip-sum/2<<endl;
    }
    return 0;
}