首页 > 代码库 > [ACM] HDU 4576 Robot （概率DP,滚动数组）

[ACM] HDU 4576 Robot （概率DP,滚动数组）

2024-07-15 08:23:42   223人阅读

Robot



Problem Description
Michael has a telecontrol robot. One day he put the robot on a loop with n cells. The cells are numbered from 1 to n clockwise.



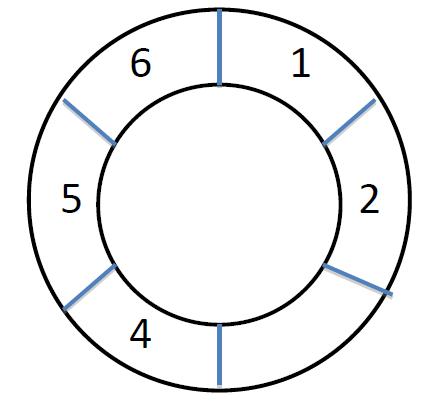
At first the robot is in cell 1. Then Michael uses a remote control to send m commands to the robot. A command will make the robot walk some distance. Unfortunately the direction part on the remote control is broken, so for every command the robot will chose a direction(clockwise or anticlockwise) randomly with equal possibility, and then walk w cells forward.
Michael wants to know the possibility of the robot stopping in the cell that cell number >= l and <= r after m commands.
 

Input
There are multiple test cases. 
Each test case contains several lines.
The first line contains four integers: above mentioned n(1≤n≤200) ,m(0≤m≤1,000,000),l,r(1≤l≤r≤n).
Then m lines follow, each representing a command. A command is a integer w(1≤w≤100) representing the cell length the robot will walk for this command.  
The input end with n=0,m=0,l=0,r=0. You should not process this test case.
 

Output
For each test case in the input, you should output a line with the expected possibility. Output should be round to 4 digits after decimal points.
 

Sample Input
3 1 1 2
1
5 2 4 4
1
2
0 0 0 0
 

Sample Output
0.5000
0.2500
 

Source
2013ACM-ICPC杭州赛区全国邀请赛


解题思路：

题意为有编号1-N的格子围城一个圈，一开始机器人站在1号格子，有M个命令，每个命令机器人走W格，可以顺时针也可以逆时针，问M个命令后，机器人站在格子[L,R] 的概率是多少.

想法大体为暴力计算出M个命令后，每个格子上机器人在的概率，那么 P[ L ] + P[ L+1] + P[ L+2] +............P[R] 即为所求

用dp[i][j] ，表示第i个命令后机器人站在j位置的概率

因为命令数m，0≤m≤1,000,000，不可能开出这么大的数组，又因为第i个命令后机器人所在位置的概率只与第i-1个命令后的机器人所在位置有关，所以可以用滚动数组，dp [2] [j]来表示。滚动数组要求当前状态只和前一个状态有关系，和更早之前的状态没关系，所以之前保存的数空间可以覆盖，重新利用，这样就可以降低空间复杂度，但时间复杂度不变。

滚动数组详解：http://blog.csdn.net/niushuai666/article/details/6677982

代码：

#include <iostream>
#include <stdio.h>
#include <iomanip>
#include <string.h>
using namespace std;
double dp[2][210];

int main()
{
    int n,m,l,r,cm;
    while(scanf("%d%d%d%d",&n,&m,&l,&r)!=EOF)
    {
        if(n==0&&m==0&&l==0&&r==0)
            break;
        int d=0;
        for(int i=1;i<n;i++)
            dp[d][i]=0;
        dp[0][0]=1;
        while(m--)
        {
            scanf("%d",&cm);
            for(int i=0;i<n;i++)
                dp[d^1][i]=0;//新状态下每个位置的概率都为0
            for(int i=0;i<n;i++)
            {
                if(dp[d][i]==0)//加上这一句就不超时了
                    continue;
                dp[d^1][(i+cm)%n]+=0.5*dp[d][i];
                dp[d^1][(i-cm+n)%n]+=0.5*dp[d][i];
            }
            d^=1;//^1 就是加1或者减1交替进行
        }
        double ans=0;
        for(int i=l-1;i<r;i++)
            ans+=dp[d][i];
        cout<<setiosflags(ios::fixed)<<setprecision(4)<<ans<<endl;
    }
    return 0;
}


联系
我们