首页 > 代码库 > Leetcode-Unique Paths
Leetcode-Unique Paths
A robot is located at the top-left corner of a m x n grid (marked ‘Start‘ in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish‘ in the diagram below).
How many possible unique paths are there?
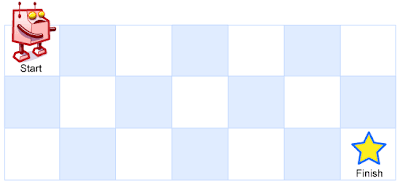
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
分析:此题第一眼想到就是DFS分别从右边格子和下边的格子各自探测然后得到结果
1 public int search(int m,int n,int cur_x,int cur_y){2 if(cur_x == m-1 && cur_y == n-1){3 return 1;4 }5 if(cur_x > m-1 || cur_y > n-1){6 return 0;7 } 8 return search(m,n,cur_x,cur_y+1) + search(m,n,cur_x+1,cur_y); 9 }
提交, 超时,我擦
再想想,递归操作因为有回溯,会有重复探测重复计算的问题,效率低
换个写法
1 public int searchNew(int m,int n){2 if(m == 1 || n == 1){3 return 1;4 } 5 return searchNew(m-1,n) + searchNew(m,n-1);6
还是递归,只不过简洁了点,但是还是超时(递归没搞清楚啊,递归必然是有重复计算的问题)
那就DP填表吧,避免重复计算,分别从1*1的矩阵一直算到m*n,开个m*n的二维数组轻松搞定
但是---忽然想到这种只需要前一步结果的填表其实不需要矩阵,省点空间,开个一维数组保存上一步的结果就行了
1 public int uniquePathsNew(int m,int n){ 2 int [] a = new int[n]; 3 for(int i = 0;i<n;i++){ 4 a[i] = 1; 5 } 6 for(int i=1;i<m;i++){ 7 for(int j = 1;j< n;j++){ 8 a[j] = a[j] + a[j-1]; 9 }10 } 11 return a[n-1];12 }
轻松AC
Leetcode-Unique Paths
声明:以上内容来自用户投稿及互联网公开渠道收集整理发布,本网站不拥有所有权,未作人工编辑处理,也不承担相关法律责任,若内容有误或涉及侵权可进行投诉: 投诉/举报 工作人员会在5个工作日内联系你,一经查实,本站将立刻删除涉嫌侵权内容。
