近期学习《算法设计与分析基础 第二版》，学习到了分治法，被课后习题吸引了，即Trimino拼图问题。想了好久，都没有想到如何去分而治之。然后就是Google到了相关的PPT。一看就明白了。自己就用代码实现了下。理解思想后，代码实现挺容易的。

    这个谜题实际上可以做成一个小益智游戏。

    分治思想的关键就在于构造相同的子问题。这是这个思想核心看似简单，实则需要对问题的洞察力。看到的PPT核心图如下：

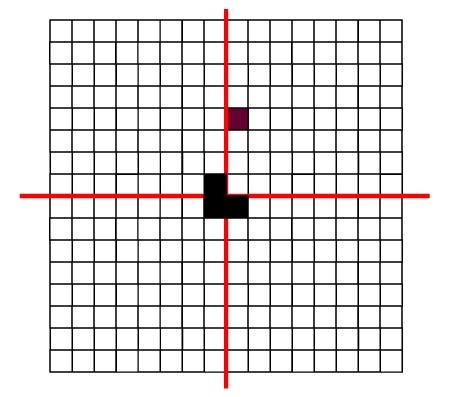
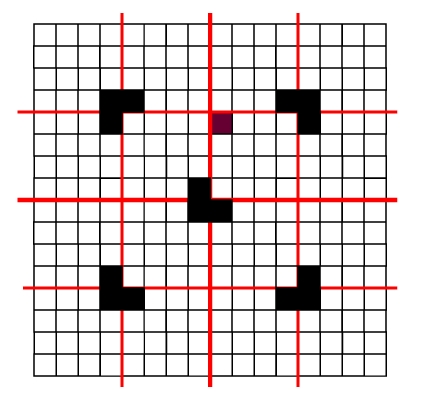
算法的源代码如下：

/**
 * @author shuaiguangying
 *	用分治法解决棋盘覆盖问题
 *  在2^n*2^n棋盘里面有一个坏点
 *  坏点可以在任何位置
 *  用L型板块覆盖棋盘
 *  
 *  解决这个问题的关键在于：分治
 *  分治的关键在于来构造有坏点的棋盘
 *  
 */
public class Tromino {
	static int numOfL = 2;
	/**
	 * @param a 棋盘
	 * @param x 子棋盘的起始位置
	 * @param y 子棋盘的起始位置
	 * @param size 子棋盘的尺寸
	 * @param bx 子棋盘中坏点的位置
	 * @param by 子棋盘中坏点的位置
	 */
	public static void trimino(Integer[][] a,int x,int y,int size,int bx,int by){
		//把一个大图分为4个小图
		int nx =x+size/2,ny =y+size/2;//十字中心
		int[] bx4 = {nx  ,nx-1,nx-1,nx};
		int[] by4 = {ny-1,ny-1,ny  ,ny};
		if(by<ny&&bx>=nx){ //坏点在第一象限
			bx4[0]=bx;by4[0]=by;
		}else if(by<ny&&bx<nx){//坏点在第二象限
			bx4[1]=bx;by4[1]=by;
		}else if(by>=ny&&bx<nx){//坏点在第三象限
			bx4[2]=bx;by4[2]=by;
		}else{//坏点在第四象限
			bx4[3]=bx;by4[3]=by;
		}
		//把L形方块图到棋盘中
		for(int i=0;i<4;i++){
			if(by4[i]==by && bx4[i]==bx)continue;
			a[by4[i]][bx4[i]]=numOfL;
		}
		numOfL++;
		//分治 递归处理子问题
		if(size>2){
			trimino(a,nx,y,size/2,bx4[0],by4[0]);
			trimino(a,x,y,size/2,bx4[1],by4[1]);
			trimino(a,x,ny,size/2,bx4[2],by4[2]);
			trimino(a,nx,ny,size/2,bx4[3],by4[3]);
		}
	}
	public static void main(String[] args) {
		int size = 8;
		Integer[][] a=new Integer[size][size];
		int bx=7,by=1;a[by][bx]=1;
		trimino(a,0,0,size,bx,by);
		
		draw(a,size);
	}
	
	private static void draw(Integer[][] a,int size){
		JFrame f = new JFrame("trimino");
		
		Integer[] head = new Integer[size];
		for (int i=0;i<head.length;i++) head[i] = i+1;
		final Color[] color =new Color[22];
		for(int i=0;i<color.length;i++){
			int r = (int) ((Math.random()*10000)%255); 
			int b =(int) ((Math.random()*1000)%255); 
			int k =(int) ((Math.random()*10000)%255); 
			color[i] = new Color(r,b,k);
		}
		
		JTable table = new JTable(a,head);
		for (int i = 0; i < table.getColumnCount(); i++) {
			TableColumn column = table.getColumn(String.valueOf(i+1));
			column.setCellRenderer(new DefaultTableCellRenderer(){
				@Override
				public Component getTableCellRendererComponent(JTable table,
						Object value, boolean isSelected, boolean hasFocus,
						int row, int column) {
					int val = (Integer)value;
					setBackground(color[val-1]);
					return super.getTableCellRendererComponent(table, value, isSelected, hasFocus,
							row, column);
				}
			});
		}
		
		table.setAutoResizeMode(JTable.AUTO_RESIZE_OFF);
		table.setRowHeight(50);
		f.getContentPane().add(table.getTableHeader(),BorderLayout.NORTH);
		f.getContentPane().add(table,BorderLayout.CENTER);
		
		f.setVisible(true);
		f.setSize(500, 500);
	}
}

为了展示算法的效果，画了一个图：

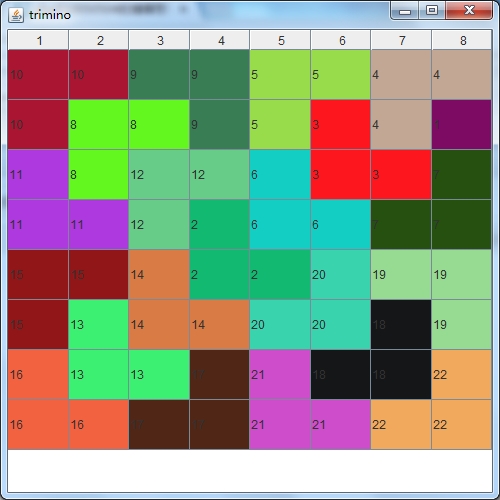
本文出自 “每天进步一点点” 博客，请务必保留此出处http://sbp810050504.blog.51cto.com/2799422/1555206

分治思想在Trimino拼图中的Java实现