图像处理之霍夫变换（直线检測算法）

霍夫变换是图像变换中的经典手段之中的一个，主要用来从图像中分离出具有某种同样特征的几何

形状（如，直线，圆等）。霍夫变换寻找直线与圆的方法相比与其他方法能够更好的降低噪

声干扰。经典的霍夫变换经常使用来检測直线，圆，椭圆等。

霍夫变换算法思想：

以直线检測为例，每一个像素坐标点经过变换都变成都直线特质有贡献的统一度量，一个简单

的样例例如以下：一条直线在图像中是一系列离散点的集合，通过一个直线的离散极坐标公式，

能够表达出直线的离散点几何等式例如以下：

X *cos(theta) + y * sin(theta)  = r 当中角度theta指r与X轴之间的夹角，r为到直线几何垂

直距离。不论什么在直线上点，x, y都能够表达，当中 r， theta是常量。该公式图形表演示样例如以下：

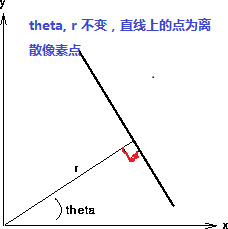
然而在实现的图像处理领域，图像的像素坐标P(x, y)是已知的，而r, theta则是我们要寻找

的变量。假设我们能绘制每一个(r, theta)值依据像素点坐标P(x, y)值的话，那么就从图像笛卡

尔坐标系统转换到极坐标霍夫空间系统，这样的从点到曲线的变换称为直线的霍夫变换。变换

通过量化霍夫參数空间为有限个值间隔等分或者累加格子。当霍夫变换算法開始，每一个像素

坐标点P(x, y)被转换到(r, theta)的曲线点上面，累加到相应的格子数据点，当一个波峰出现

时候，说明有直线存在。相同的原理，我们能够用来检測圆，仅仅是对于圆的參数方程变为如

下等式：

(x –a ) ^2 + (y-b) ^ 2 = r^2当中(a, b)为圆的中心点坐标，r圆的半径。这样霍夫的參数空间就

变成一个三维參数空间。给定圆半径转为二维霍夫參数空间，变换相对简单，也比較经常使用。

编程思路解析：

1.      读取一幅带处理二值图像，最好背景为黑色。

2.      取得源像素数据

3.      依据直线的霍夫变换公式完毕霍夫变换，预览霍夫空间结果

4.       寻找最大霍夫值，设置阈值，反变换到图像RGB值空间(程序难点之中的一个)

5.      越界处理，显示霍夫变换处理以后的图像

关键代码解析：

直线的变换角度为[0 ~ PI]之间，设置等份为500为PI/500，同一时候依据參数直线參数方程的取值

范围为[-r, r]有例如以下霍夫參数定义：

 // prepare for hough transform
 int centerX = width / 2;
 int centerY = height / 2;
 double hough_interval = PI_VALUE/(double)hough_space;
	    
 int max = Math.max(width, height);
 int max_length = (int)(Math.sqrt(2.0D) * max);
 hough_1d = new int[2 * hough_space * max_length];

实现从像素RGB空间到霍夫空间变换的代码为：

// start hough transform now....
int[][] image_2d = convert1Dto2D(inPixels);
for (int row = 0; row < height; row++) {
	for (int col = 0; col < width; col++) {
    	int p = image_2d[row][col] & 0xff;
    	if(p == 0) continue; // which means background color
    	
    	// since we does not know the theta angle and r value, 
    	// we have to calculate all hough space for each pixel point
    	// then we got the max possible theta and r pair.
    	// r = x * cos(theta) + y * sin(theta)
    	for(int cell=0; cell < hough_space; cell++ ) {
    		max = (int)((col - centerX) * Math.cos(cell * hough_interval) + (row - centerY) * Math.sin(cell * hough_interval));
    		max += max_length; // start from zero, not (-max_length)
    		if (max < 0 || (max >= 2 * max_length)) {// make sure r did not out of scope[0, 2*max_lenght]
                continue;
            }
    		hough_2d[cell][max] +=1;
    	}
    }
}

寻找最大霍夫值计算霍夫阈值的代码例如以下：

// find the max hough value
int max_hough = 0;
for(int i=0; i<hough_space; i++) {
	for(int j=0; j<2*max_length; j++) {
		hough_1d[(i + j * hough_space)] = hough_2d[i][j];
		if(hough_2d[i][j] > max_hough) {
			max_hough = hough_2d[i][j];
		}
	}
}
System.out.println("MAX HOUGH VALUE = http://www.mamicode.com/" + max_hough);>
从霍夫空间反变换回像素数据空间代码例如以下：
	    // transfer back to image pixels space from hough parameter space
	    int hough_threshold = (int)(threshold * max_hough);
	    for(int row = 0; row < hough_space; row++) {
	    	for(int col = 0; col < 2*max_length; col++) {
	    		if(hough_2d[row][col] < hough_threshold) // discard it
	    			continue;
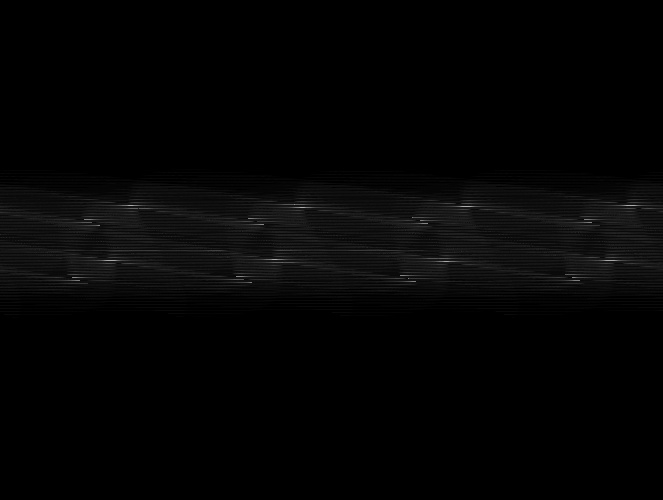
	    		int hough_value = http://www.mamicode.com/hough_2d[row][col];>霍夫变换源图例如以下：

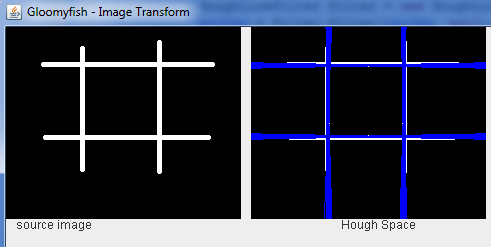
霍夫变换以后，在霍夫空间显演示样例如以下：（白色表示已经找到直线信号）

终于反变换回到像素空间效果例如以下：

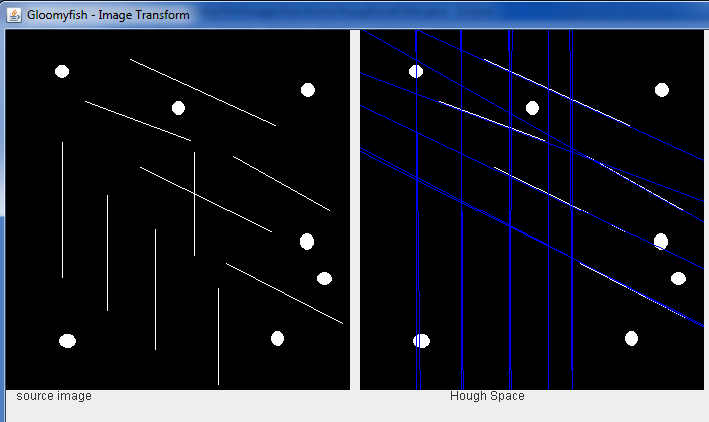
一个更好的执行监測直线的结果(输入为二值图像)：

完整的霍夫变换源码例如以下：
package com.gloomyfish.image.transform;

import java.awt.image.BufferedImage;

import com.process.blur.study.AbstractBufferedImageOp;

public class HoughLineFilter extends AbstractBufferedImageOp {
	public final static double PI_VALUE = http://www.mamicode.com/Math.PI;>转载文章请务必注明出自本博客！！