首页 > 代码库 > 最短路径--SPFA 算法
最短路径--SPFA 算法
适用范围:给定的图存在负权边,这时类似Dijkstra等算法便没有了用武之地,而Bellman-Ford算法的复杂度又过高,SPFA算法便派上用场了。 我们约定有向加权图G不存在负权回路,即最短路径一定存在。当然,我们可以在执行该算法前做一次拓扑排序,以判断是否存在负权回路,但这不是我们讨论的重点。
算法思想:我们用数组d记录每个结点的最短路径估计值,用邻接表来存储图G。我们采取的方法是动态逼近法:设立一个先进先出的队列用来保存待优化的结点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止
期望的时间复杂度O(ke), 其中k为所有顶点进队的平均次数,可以证明k一般小于等于2。
实现方法:
建立一个队列,初始时队列里只有起始点,再建立一个表格记录起始点到所有点的最短路径(该表格的初始值要赋为极大值,该点到他本身的路径赋为0)。然后执行松弛操作,用队列里有的点作为起始点去刷新到所有点的最短路,如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。
判断有无负环:
如果某个点进入队列的次数超过N次则存在负环(SPFA无法处理带负环的图)

首先建立起始点a到其余各点的
最短路径表格
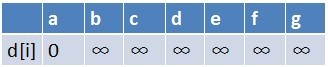
首先源点a入队,当队列非空时:
1、队首元素(a)出队,对以a为起始点的所有边的终点依次进行松弛操作(此处有b,c,d三个点),此时路径表格状态为:
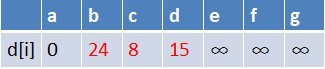
在松弛时三个点的最短路径估值变小了,而这些点队列中都没有出现,这些点
需要入队,此时,队列中新入队了三个结点b,c,d
队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e点),此时路径表格状态为:
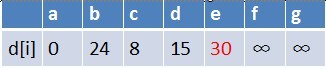
在最短路径表中,e的最短路径估值也变小了,e在队列中不存在,因此e也要
入队,此时队列中的元素为c,d,e
队首元素c点出队,对以c为起始点的所有边的终点依次进行松弛操作(此处有e,f两个点),此时路径表格状态为:
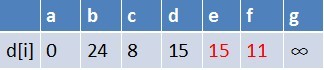
在最短路径表中,e,f的最短路径估值变小了,e在队列中存在,f不存在。因此
e不用入队了,f要入队,此时队列中的元素为d,e,f
队首元素d点出队,对以d为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:
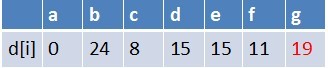
在最短路径表中,g的最短路径估值没有变小(松弛不成功),没有新结点入队,队列中元素为f,g
队首元素f点出队,对以f为起始点的所有边的终点依次进行松弛操作(此处有d,e,g三个点),此时路径表格状态为:

在最短路径表中,e,g的最短路径估值又变小,队列中无e点,e入队,队列中存在g这个点,g不用入队,此时队列中元素为g,e
队首元素g点出队,对以g为起始点的所有边的终点依次进行松弛操作(此处只有b点),此时路径表格状态为:
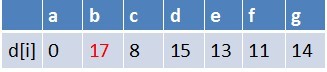
在最短路径表中,b的最短路径估值又变小,队列中无b点,b入队,此时队列中元素为e,b
队首元素e点出队,对以e为起始点的所有边的终点依次进行松弛操作(此处只有g这个点),此时路径表格状态为:
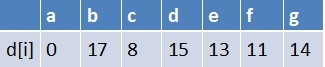
在最短路径表中,g的最短路径估值没变化(松弛不成功),此时队列中元素为b
队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e这个点),此时路径表格状态为:

在最短路径表中,e的最短路径估值没变化(松弛不成功),此时队列为空了
最终a到g的最短路径为14
SPFA优化算法:
/*
SPFA(Shortest Path Faster Algorithm) [图的存储方式为邻接表]
是Bellman-Ford算法的一种队列实现,减少了不必要的冗余计算。
算法大致流程是用一个队列来进行维护。 初始时将源加入队列。 每次从队列中取出一个元素,
并对所有与他相邻的点进行松弛,若某个相邻的点松弛成功,则将其入队。 直到队列为空时算法结束。
它可以在O(kE)的时间复杂度内求出源点到其他所有点的最短路径,可以处理负边。
SPFA 在形式上和BFS非常类似,不同的是BFS中一个点出了队列就不可能重新进入队列,但是SPFA中
一个点可能在出队列之后再次被放入队列,也就是一个点改进过其它的点之后,过了一段时间可能本
身被改进,于是再次用来改进其它的点,这样反复迭代下去。
判断有无负环:如果某个点进入队列的次数超过V次则存在负环(SPFA无法处理带负环的图)。
SPFA算法有两个优化算法 SLF 和 LLL:
SLF:Small Label First 策略,设要加入的节点是j,队首元素为i,若dist(j)<dist(i),则将j插入队首,
否则插入队尾。
LLL:Large Label Last 策略,设队首元素为i,队列中所有dist值的平均值为x,若dist(i)>x则将i插入
到队尾,查找下一元素,直到找到某一i使得dist(i)<=x,则将i出对进行松弛操作。
引用网上资料,SLF 可使速度提高 15 ~ 20%;SLF + LLL 可提高约 50%。
在实际的应用中SPFA的算法时间效率不是很稳定,为了避免最坏情况的出现,通常使用效率更加稳定的Dijkstra算法。
*/
1 //用数组实现邻接表存储,pnt[i,0]表示与i相邻的结点个数,pnt[i,1...k]存储与i相邻的点 2 int pnt[MAXN][MAXN]; 3 int map[MAXN][MAXN]; //map[i,j]为初始输入的i到j的距离,并且map[i,i]=0;未知的map[i,j]=INF; 4 int dis[MAXN]; 5 char vst[MAXN]; 6 7 int SPFA(int n,int s) 8 { 9 int i, pri, end, p, t; 10 memset(vst, 0, sizeof(vst)); 11 for (i=1; i<=n; i++) 12 dis[i] = INF; 13 dis[s] = 0; 14 vst[s] = 1; 15 Q[0] = s; pri = 0; end = 1; 16 while (pri < end) 17 { 18 p = Q[pri]; 19 for (i=1; i<=pnt[p][0]; i++) 20 { 21 t = pnt[p][i]; 22 //先释放,释放成功后再判断是否要加入队列 23 if (dis[p]+map[p][t] < dis[t]) 24 { 25 dis[t] = dis[p]+map[p][t]; 26 if (!vst[t]) 27 { 28 Q[end++] = t; 29 vst[t] = 1; 30 } 31 } 32 } 33 vst[p] = 0; 34 pri++; 35 } 36 return 1; 37 }
1 正规邻接表存储: 2 /* ------- 邻接表存储 ----------- */ 3 struct Edge 4 { 5 int e; //终点 6 int v; //边权 7 struct Edge *nxt; 8 }; 9 struct 10 { 11 struct Edge *head, *last; 12 } node[MAXN]; 13 /* -------------------------------- */ 14 15 /* 添加有向边<起点,终点,边权> */ 16 void add(int s,int e,int v) 17 { 18 struct Edge *p; 19 p = (struct Edge*)malloc(sizeof(struct Edge)); 20 p->e = e; 21 p->v = v; 22 p->nxt = NULL; 23 if (node[s].head == NULL) 24 { 25 node[s].head = p; 26 node[s].last = p; 27 } 28 else 29 { 30 node[s].last->nxt = p; 31 node[s].last = p; 32 } 33 } 34 35 /* 松弛,成功返回1,否则0 */ 36 int relax(int s,int e,int v) 37 { 38 if (dis[s]+v < dis[e]) 39 { 40 dis[e] = dis[s]+v; 41 return 1; 42 } 43 return 0; 44 } 45 46 /* SPFA有负权回路返回0,否则返回1并且最短路径保存在dis[] */ 47 int n; 48 int vst[MAXN], cnt[MAXN]; 49 int Q[MAXN*MAXN]; 50 int SPFA(int s0) 51 { 52 int i, p, q; 53 struct Edge *pp; 54 55 memset(vst, 0, sizeof(vst)); 56 memset(cnt, 0, sizeof(cnt)); 57 for (i=0; i<=n; i++) 58 dis[i] = INF; 59 dis[s0] = 0; 60 61 Q[0] = s0; p = 0; q = 1; 62 vst[s0] = 1; 63 cnt[s0]++; 64 while (p < q) 65 { 66 pp = node[Q[p]].head; 67 while (pp) 68 { 69 if (relax(Q[p], pp->e, pp->v) && !vst[pp->e]) 70 { 71 Q[q++] = pp->e; 72 vst[pp->e] = 1; 73 cnt[pp->e]++; 74 if (cnt[pp->e] > n) //有负权回路 75 return 0; 76 } 77 pp = pp->nxt; 78 } 79 vst[Q[p]] = 0; 80 p++; 81 } 82 return 1; 83 }
1 /**通过poj 3159 证明:还是用数组来实现邻接表比用链表来实现邻接表效率高, **/ 2 3 #define MAX_node 10000 4 #define MAX_edge 100000 5 6 struct Edge 7 { 8 int e, v; 9 } edge[MAX_edge]; 10 11 int neg; //number of edge 12 int node[MAX_node]; //注意node要用memset初始化全部为-1 13 int next[MAX_edge]; 14 15 void add(int s,int e,int v) 16 { 17 edge[neg].e = e; 18 edge[neg].v = v; 19 next[neg] = node[s]; 20 node[s] = neg++; 21 } 22 /* 该题还证明用栈来实现SPFA比用队列来实现效率高,还节约空间 */ 23 int SPFA(int s0)//栈实现 24 { 25 int i, t, p, top; 26 27 memset(vst, 0, sizeof(vst)); 28 for (i=1; i<=n; i++) 29 dis[i] = INF; 30 dis[s0] = 0; 31 32 Q[0] = s0; 33 top = 1; 34 vst[s0] = 1; 35 while (top) 36 { 37 t = Q[--top]; 38 vst[t] = 0; 39 p = node[t]; 40 while (p != -1) 41 { 42 if (relax(t, edge[p].e, edge[p].v) && !vst[edge[p].e]) 43 { 44 Q[top++] = edge[p].e; 45 vst[edge[p].e] = 1; 46 } 47 p = next[p]; 48 } 49 } 50 return 1; 51 }
- /*
- SPFA(Shortest Path Faster Algorithm) [图的存储方式为邻接表]
- 是Bellman-Ford算法的一种队列实现,减少了不必要的冗余计算。
- 算法大致流程是用一个队列来进行维护。 初始时将源加入队列。 每次从队列中取出一个元素,
- 并对所有与他相邻的点进行松弛,若某个相邻的点松弛成功,则将其入队。 直到队列为空时算法结束。
- 它可以在O(kE)的时间复杂度内求出源点到其他所有点的最短路径,可以处理负边。
- SPFA 在形式上和BFS非常类似,不同的是BFS中一个点出了队列就不可能重新进入队列,但是SPFA中
- 一个点可能在出队列之后再次被放入队列,也就是一个点改进过其它的点之后,过了一段时间可能本
- 身被改进,于是再次用来改进其它的点,这样反复迭代下去。
- 判断有无负环:如果某个点进入队列的次数超过V次则存在负环(SPFA无法处理带负环的图)。
- SPFA算法有两个优化算法 SLF 和 LLL:
- SLF:Small Label First 策略,设要加入的节点是j,队首元素为i,若dist(j)<dist(i),则将j插入队首,
- 否则插入队尾。
- LLL:Large Label Last 策略,设队首元素为i,队列中所有dist值的平均值为x,若dist(i)>x则将i插入
- 到队尾,查找下一元素,直到找到某一i使得dist(i)<=x,则将i出对进行松弛操作。
- 引用网上资料,SLF 可使速度提高 15 ~ 20%;SLF + LLL 可提高约 50%。
- 在实际的应用中SPFA的算法时间效率不是很稳定,为了避免最坏情况的出现,通常使用效率更加稳定的Dijkstra算法。
- */
- //用数组实现邻接表存储,pnt[i,0]表示与i相邻的结点个数,pnt[i,1...k]存储与i相邻的点
- int pnt[MAXN][MAXN];
- int map[MAXN][MAXN]; //map[i,j]为初始输入的i到j的距离,并且map[i,i]=0;未知的map[i,j]=INF;
- int dis[MAXN];
- char vst[MAXN];
- int SPFA(int n,int s)
- {
- int i, pri, end, p, t;
- memset(vst, 0, sizeof(vst));
- for (i=1; i<=n; i++)
- dis[i] = INF;
- dis[s] = 0;
- vst[s] = 1;
- Q[0] = s; pri = 0; end = 1;
- while (pri < end)
- {
- p = Q[pri];
- for (i=1; i<=pnt[p][0]; i++)
- {
- t = pnt[p][i];
- //先释放,释放成功后再判断是否要加入队列
- if (dis[p]+map[p][t] < dis[t])
- {
- dis[t] = dis[p]+map[p][t];
- if (!vst[t])
- {
- Q[end++] = t;
- vst[t] = 1;
- }
- }
- }
- vst[p] = 0;
- pri++;
- }
- return 1;
- }
最短路径--SPFA 算法
