BP（Back Propagation）网络是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是眼下应用最广泛的神经网络模型之中的一个。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描写叙述这样的映射关系的数学方程。

一个神经网络的结构示意图例如以下所看到的。

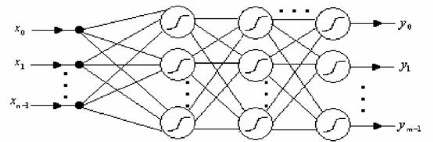
BP神经网络模型拓扑结构包括输入层（input）、隐层(hide layer)和输出层(output layer)。输入层神经元的个数由样本属性的维度决定，输出层神经元的个数由样本分类个数决定。隐藏层的层数和每层的神经元个数由用户指定。每一层包括若干个神经元，每一个神经元包括一个而阈值，用来改变神经元的活性。网络中的弧线表示前一层神经元和后一层神经元之间的权值。每一个神经元都有输入和输出。输入层的输入和输出都是训练样本的属性值。

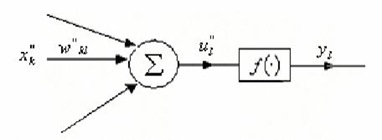
对于隐藏层和输出层的输入 当中，是由上一层的单元i到单元j的连接的权；是上一层的单元i的输出；而是单元j的阈值。

神经网络中神经元的输出是经由赋活函数计算得到的。该函数用符号表现单元代表的神经元活性。赋活函数一般使用simoid函数（或者logistic函数）。神经元的输出为：

除此之外，神经网络中有一个学习率（l）的概念，通常取0和1之间的值，并有助于找到全局最小。假设学习率太小，学习将进行得非常慢。假设学习率太大，可能出如今不适当的解之间摆动。

交代清楚了神经网络中基本要素，我们来看一下BP算法的学习过程：

BPTrain(){

      初始化network的权和阈值。

      while 终止条件不满足 {

            for samples中的每一个训练样本X {

            // 向前传播输入

            for 隐藏或输出层每一个单元j {

                  ；// 相对于前一层i，计算单元j的净输入 ；// 计算单元j的输出

            }

            // 后向传播误差

            for 输出层每一个单元j {

                  ；// 计算误差

            }

            for 由最后一个到第一个隐藏层，对于隐藏层每一个单元j {

                   ；// k是j的下一层中的神经元

            }

            for network中每一个权 {

                    ； // 权增值

                    ； // 权更新

             }

             for network中每一个偏差 {

                      ； // 偏差增值

                      ；// 偏差更新

             }

      }

}

算法基本流程就是：

1、初始化网络权值和神经元的阈值（最简单的办法就是随机初始化）

2、前向传播：依照公式一层一层的计算隐层神经元和输出层神经元的输入和输出。

3、后向传播：依据公式修正权值和阈值

直到满足终止条件。

算法中还有几点是须要说明的：

1、关于，是神经元的误差。

对于输出层神经元，当中，是单元j的实际输 出，而是j基于给定训练样本的已知类标号的真正输出。

对于隐藏层神经元，当中，是由下一较高层中单元k到单元j的连接权，而是单元k的误差。

权值增量是，阈值增量是，当中是学习率。

对于的推导採用了梯度下降的算法。推导的前提是保证输出单元的均方差最小。，当中P是样本总数，m是输出层神经元个数是样本实际输出，是神经网络输出。

梯度下降思路就是对求的导数。

对于输出层：

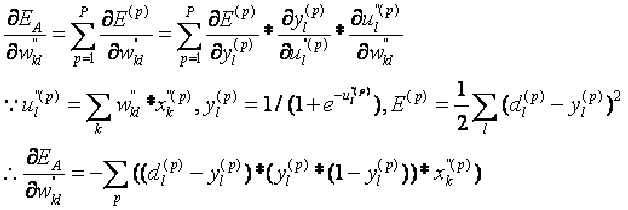
当中的就是。

对于隐藏层：

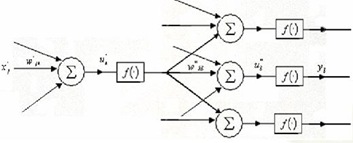
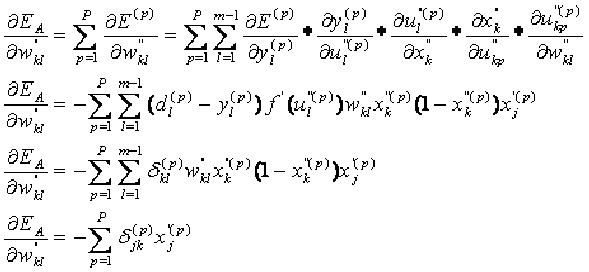
当中=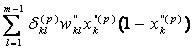就是隐藏层的误差计算公式。

2、关于终止条件，能够有多种形式：

§ 前一周期全部的都太小，小于某个指定的阈值。

§ 前一周期未正确分类的样本百分比小于某个阈值。

§ 超过预先指定的周期数。

§ 神经网络的输出值和实际输出值的均方误差小于某一阈值。

一般地，最后一种终止条件的准确率更高一些。

在实际使用BP神经网络的过程中，还会有一些实际的问题：

1、 样本处理。对于输出，假设仅仅有两类那么输出为0和1，仅仅有当趋于正负无穷大的时候才会输出0，1。因此条件可适当放宽，输出>0.9时就觉得是1，输出<0.1时觉得是0。对于输入，样本也须要做归一化处理。

2、 网络结构的选择。主要是指隐藏层层数和神经元数决定了网络规模，网络规模和性能学习效果密切相关。规模大，计算量大，并且可能导致过度拟合；可是规模小，也可能导致欠拟合。

3、 初始权值、阈值的选择，初始值对学习结果是有影响的，选择一个合适初始值也很重要。

4、 增量学习和批量学习。上面的算法和数学推导都是基于批量学习的，批量学习适用于离线学习，学习效果稳定性好；增量学习使用于在线学习，它对输入样本的噪声是比較敏感的，不适合剧烈变化的输入模式。

5、 对于激励函数和误差函数也有其它的选择。

总的来说BP算法的可选项比較多，针对特定的训练数据往往有比較大的优化空间。