首页 > 代码库 > 最优化问题（牛顿法和梯度下降法）
最优化问题（牛顿法和梯度下降法）
---恢复内容开始---
http://www.zhihu.com/question/19723347
引自知乎
牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。
根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。
wiki上给的图很形象：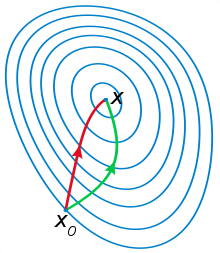
红色的牛顿法的迭代路径，绿色的是梯度下降法的迭代路径。
根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。
wiki上给的图很形象：
红色的牛顿法的迭代路径，绿色的是梯度下降法的迭代路径。作者：金秉文
链接：http://www.zhihu.com/question/19723347/answer/14636244
来源：知乎
著作权归作者所有，转载请联系作者获得授权。
1牛顿法起始点不能离局部极小点太远，否则很可能不会收敛。(考虑到二阶拟合应该很容易想象)，所以实际操作中会先使用别的方法，比如梯度下降法，使更新的点离最优点比较近，再开始用牛顿法。
2. 牛顿法每次需要更新一个二阶矩阵，当维数增加的时候是非常耗内存的，所以实际使用是会用拟牛顿法。
3. 梯度下降法在非常靠近最优点时会有震荡，就是说明明离的很近了，却很难到达，因为线性的逼近非常容易一个方向过去就过了最优点(因为只能是负梯度方向)。但牛顿法因为是二次收敛就很容易到达了。
牛顿法最明显快的特点是对于二阶函数(考虑多元函数的话要在凸函数的情况下)，牛顿法能够一步到达，非常有效。
2. 牛顿法每次需要更新一个二阶矩阵，当维数增加的时候是非常耗内存的，所以实际使用是会用拟牛顿法。
3. 梯度下降法在非常靠近最优点时会有震荡，就是说明明离的很近了，却很难到达，因为线性的逼近非常容易一个方向过去就过了最优点(因为只能是负梯度方向)。但牛顿法因为是二次收敛就很容易到达了。
牛顿法最明显快的特点是对于二阶函数(考虑多元函数的话要在凸函数的情况下)，牛顿法能够一步到达，非常有效。
作者：刘熙昶
链接：http://www.zhihu.com/question/19723347/answer/28414541
来源：知乎
著作权归作者所有，转载请联系作者获得授权。
最爱麦丽素这篇知乎问答中的一个科普性的全面回答
---恢复内容结束---
最优化问题（牛顿法和梯度下降法）
声明：以上内容来自用户投稿及互联网公开渠道收集整理发布，本网站不拥有所有权，未作人工编辑处理，也不承担相关法律责任，若内容有误或涉及侵权可进行投诉： 投诉/举报 工作人员会在5个工作日内联系你，一经查实，本站将立刻删除涉嫌侵权内容。