一、概述

Erasure Code可以应用于分布式存储系统中，替代多份数据拷贝的数据冗余方式，从而可以提高存储空间利用率。此外，Erasure code还可以应用于传统RAID系统中，增加数据冗余度，支持多块盘同时发生故障，从而可以提高数据可靠性。

采用范德蒙矩阵可以构建Erasure code（关于范德蒙矩阵的编解码方法，可以参考文章《基于范德蒙矩阵的Erasure code技术详解》），其生成矩阵表示如下：

采用范德蒙矩阵作为编码矩阵的问题在于算法复杂度太高，其解码算法复杂度为O（n^3）。采用目前的处理器技术，还是会影响IO的性能，增加IO延迟。因此，找到一种更加合理的编码矩阵，降低算法复杂度是Erasure code得以广泛应用的一个前提条件。

二、基于柯西矩阵的编解码过程

基于柯西矩阵的李德-所罗门（RS）码是在范德蒙矩阵的RS码基础上作了两点重要改进：

1，用柯西矩阵来代替范德蒙矩阵。由于范德蒙矩阵求逆运算的复杂度为O（n^3），而柯西矩阵求逆运算的复杂度仅为O（n^2）。因此，采用柯西矩阵可以降低解码的运算复杂度。

2，采用有限域二进制矩阵的方式来提高运算效率，直接将乘法转换成XOR逻辑运算，大大降低了运算复杂度。

大家知道，柯西矩阵可以描述如下：

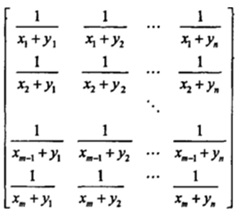
X（i）和Y（i）都是迦罗华域GF（2^w）中的元素。柯西矩阵有两个特点：第一，任意一个子方阵都是奇异矩阵，存在逆矩阵；第二，柯西矩阵在迦罗华域上的求逆运算，可以在O（n^2）的运算复杂度内完成。

采用柯西矩阵进行Erasure code编码过程描述如下：

其运算过程和范德蒙矩阵编码过程是一样的，只不过采用柯西矩阵替换了范德蒙矩阵。从运算过程来看，编码过程是迦罗华域的系列乘法、加法运算。

柯西解码方程描述如下：

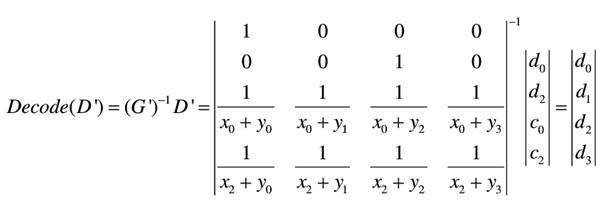
当任何一个数据元d（i）遭到损坏时，需要通过解码过程进行数据恢复。数据解码过程可以分成如下几大步骤：

1，选取剩余有效的数据块，构成一个解码列向量。例如，d1、d3数据块损坏了，那么可以选取剩余数据d0、d2、c0、c2作为解码列向量。

2，摘取生成矩阵（柯西矩阵）中解码列向量所对应的行，构成方阵A，该矩阵的逆矩阵就是解码生成矩阵inv(A)。

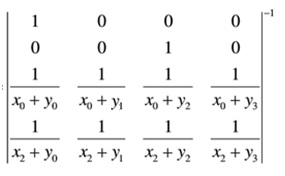
3，解码生成矩阵inv(A)和解码列向量的乘积就可以得到丢失的数据d1和d3。

从整个过程来看，矩阵求逆过程是最大的运算开销。解码过程和范德蒙矩阵编码是一样的，但是柯西矩阵的求逆运算复杂度要低于范德蒙矩阵，因此，具有更好的性能。

三、柯西编解码过程优化

从编解码过程来看，柯西编解码最大的运算量是乘法和加法运算。在范德蒙编码的时候，我们可以采用对数/反对数表的方法将乘法运算转换成了加法运算，并且在迦罗华域中，加法运算转换成了XOR运算。

柯西编解码为了降低乘法复杂度，采用了有限域上的元素都可以使用二进制矩阵表示的原理，将乘法运算转换成了迦罗华域“与运算”和“XOR逻辑运算”，提高了编解码效率。

从数学的角度来看，在迦罗华有限域中，任何一个GF（2^w）域上的元素都可以映射到GF（2）二进制域，并且采用一个二进制矩阵的方式表示GF（2^w）中的元素。例如，GF（2^3）域中的元素可以表示成GF（2）域中的二进制矩阵：

图中，黑色方块表示逻辑1，白色方块表示逻辑0。通过这种转换，GF（2^w）域中的阵列就可以转换成GF（2）域中的二进制阵列。生成矩阵的阵列转换表示如下：

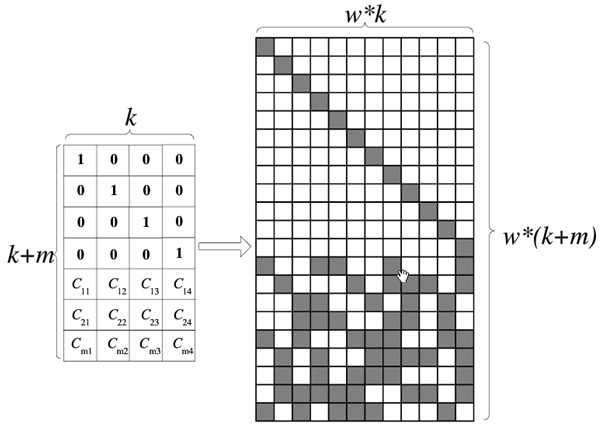
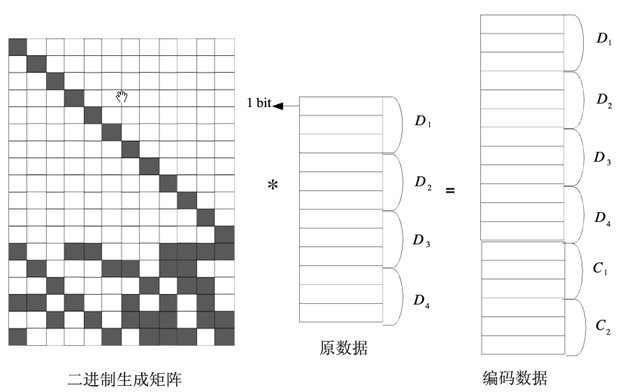
在GF（2^w）域中的生成矩阵为K*（K+m），转换到GF（2）域中，变成了(w*k) * (w*(k+m))二进制矩阵。采用域转换的目的是简化GF（2^w）域中的乘法运算。在GF（2）域中，乘法运算变成了逻辑与运算，加法运算变成了XOR运算，可以大大降低运算复杂度。和范德蒙编解码中提到的对数/反对数方法相比，这种方法不需要构建对数/反对数表，可以支持w为很大的GF域空间。采用这种有限域转换的方法之后，柯西编码运算可以表示如下：

四、总结

可以说柯西编码是在范德蒙编码基础之上的一种优化。其主要有两点：第一降低了矩阵求逆的运算复杂度；第二通过有限域转换，将GF（2^w）域中的元素转换成二进制矩阵，简化了乘法运算。所以，柯西编解码要优于范德蒙矩阵的方法，柯西编码的运算复杂度为O（n(n- m)），解码复杂度为O（n^2）。

本文出自 “存储之道” 博客，转载请与作者联系！