首页 > 代码库 > 剑指offer源码系列-变态跳台阶

剑指offer源码系列-变态跳台阶

2024-08-06 07:54:09   221人阅读

题目1389：变态跳台阶
时间限制：1 秒内存限制：32 兆特殊判题：否提交：1906解决：1102
题目描述：
一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
输入：
输入可能包含多个测试样例，对于每个测试案例，
输入包括一个整数n(1<=n<=50)。
输出：
对应每个测试案例，
输出该青蛙跳上一个n级的台阶总共有多少种跳法。
样例输入：
6
样例输出：

32




解法分析：

 分析：用Fib(n)表示青蛙跳上n阶台阶的跳法数，青蛙一次性跳上n阶台阶的跳法数1(n阶跳)，设定Fib(0) = 1；
       当n = 1 时， 只有一种跳法，即1阶跳：Fib(1) = 1;
       当n = 2 时， 有两种跳的方式，一阶跳和二阶跳：Fib(2) = Fib(1) + Fib(0) = 2;
       当n = 3 时，有三种跳的方式，第一次跳出一阶后，后面还有Fib(3-1)中跳法； 第一次跳出二阶后，后面还有Fib(3-2)中跳法；第一次跳出三阶后，后面还有Fib(3-3)中跳法
        Fib(3) = Fib(2) + Fib(1)+Fib(0)=4;
       当n = n 时，共有n种跳的方式，第一次跳出一阶后，后面还有Fib(n-1)中跳法； 第一次跳出二阶后，后面还有Fib(n-2)中跳法..........................第一次跳出n阶后，后面还有 Fib(n-n)中跳法.
       Fib(n) = Fib(n-1)+Fib(n-2)+Fib(n-3)+..........+Fib(n-n)=Fib(0)+Fib(1)+Fib(2)+.......+Fib(n-1)
      又因为Fib(n-1)=Fib(0)+Fib(1)+Fib(2)+.......+Fib(n-2)
      两式相减得：Fib(n)-Fib(n-1)=Fib(n-1)         =====》  Fib(n) = 2*Fib(n-1)     n >= 2
      递归等式如下：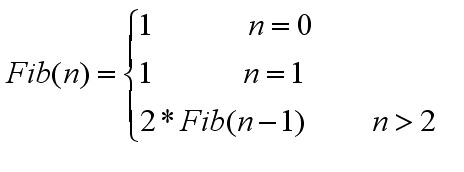


#include<iostream>
#include<stdio.h>
using namespace std;
//递归
long  long f(int n){
    if(n==0)return 1;
    if(n==1)return 1;
    return 2*f(n-1);
}
int main(){
    int n;
    while(scanf("%d",&n)!=EOF){
        printf("%ld\n",f(n));
    }
    return 0;
}


剑指offer源码系列-变态跳台阶


联系
我们