这是一个众所周知的小游戏，玩法我想大家都知道，小时候，我们通常是这样玩，两个人，每人手里一摞牌，两人分别抽出两张，共4张牌，用这4张牌计算24点，如果无法算出24点的牌，要各自收回，否则，先算出24点的人报出24点的算法并让对方收下这4张牌。这样，计算反应慢点的人往往手里的牌会越来越多。

  大二的时候，记得有同学问我1,3,4,6，怎么计算24点，冥思苦想了半天，不得其解，那个时候并没想到去网络上找找答案，只是想着编个程序试试能否找到答案。说到互联网。不可否认，网络让我们处在一个知识爆炸的年代，同时也让我们变得慵懒浮躁，我们开始倾向于从百度窗口中找到你想要的答案，而不愿意通过思考去获取问题的答案。没有比通过自己思考和努力获得问题的答案最使人欢欣鼓舞，比如我大学最喜欢的游戏，暗黑2，从1级开始一级一级的练，打完普通模式打地狱模式，经常在一个又一个打怪升级的任务中转晕了脑袋，其中的乐趣来自不断的升级，技能提升，爆装备和任务的完成。自从下载了网上的变态存档后，只要一现身，放佛启用了霸王色霸气，周边小怪物直接倒下，连最终boss巴赫都弱爆了，那时候，突然感觉不再爱了，至今未再碰暗黑2，哪一天老了，想再怀旧一下或许会再打开试试。

  言归正传，如何用计算机去计算结果呢，我希望用比较简洁的方式去解决

    假设有四张牌 A ,B ,C, D ，不管怎么计算，总有两张牌先计算，我们用排列组合的方式取两张牌计算，把计算的结果看做一张牌，那么手里还有三张牌，对这三张牌再次进行排列组合取两张牌计算，最后，将剩下的两张牌进行计算，看看能否取得最终结果24点

    由4张牌3运算操作可以得到，整个运算过程全部枚举的话，需要7重循环，代码会相当臃肿，这里暂时先用递归来代替。

   首先枚举出一个牌的排列，然后对这个排列，枚举出所有运算操作的排列，以此运算，看能够得到目标结果。

   对于每一个牌的排列，假设为A,B,C,D，它的运算无非有如下几种情形

   (A※B)※(C※D)

   ((A※B)※C)※D

  (A※(B※C))※D

   A※((B※C)※D)

   A※(B※(C※D))

其中，,※表示任意运算符号，代码如下

#include <string.h> 
#include <math.h>

#define MAX_CARDS     10 
#define CARDS_NUM     4 
#define OPT_NUM       4 
#define MAX_CAL       24 
#define MAX_DEL       0.01

int p_array[MAX_CARDS] = {1,2,3,4}; 
int used_array[MAX_CARDS]={0}; 
char opt_smobol[OPT_NUM+1] = {"+-*/"}; 
int opt_array[CARDS_NUM-1] = {0}; 
int input[CARDS_NUM] ={1,3,4,6};  //待计算的牌 
const char dbg_string[5][26] ={ 
"(%d %c%d)%c(%d%c%d)", 
"((%d%c%d)%c%d)%c%d", 
"(%d%c(%d%c%d))%c%d", 
"%d%c((%d%c%d)%c%d)", 
"%d%c(%d%c(%d%c%d))"}; 
/*计算A，B，根据opt运算*/

double cal(double a,double b,int opt) 
{ 
    switch(opt) 
    { 
    case 0: return a+b; 
    case 1:return a-b; 
    case 2:return a*b; 
    case 3: 
        return b==0.0?0:a/b; 
    } 
    return 0;               
}

/*检测是否为24，由于由除法运算，必须允许部分误差*/ 
bool check_24(double rst) 
{ 
    rst -= 24.0; 
    rst =fabs(rst); 
    if(rst<MAX_DEL) return true; 
    return false; 
}

/*检验结果并输出运算过程*/ 
void check_rst(int *array,int *opt_array,double *rst_array) 
{ 
    for(int i=0;i<5;i++) 
    { 
        if(check_24(rst_array[i])) 
        { 
            printf(dbg_string[i],input[array[0]-1],opt_smobol[opt_array[0]], 
                              input[array[1]-1],opt_smobol[opt_array[1]], 
                              input[array[2]-1],opt_smobol[opt_array[2]], 
                              input[array[3]-1] 
                              ); 
            printf("\n"); 
        } 
    }

} 
/*输入一个牌的排列，计算结果 
   (A※B)※(C※D)

   ((A※B)※C)※D

  (A※(B※C))※D

   A※((B※C)※D)

   A※(B※(C※D)) 
*/ 
void cal_result(int *array,int *opt_array,int idx) 
{ 
      int i; 
      int A,B,C,D;   
      double A_B; 
      double B_C; 
      double C_D; 
      double rst[5]; //五种运算的不同结果存储在数组中

      if(idx==(CARDS_NUM-1)) 
      { 
         A = input[array[0]-1]; 
         B = input[array[1]-1]; 
         C = input[array[2]-1]; 
         D = input[array[3]-1]; 
         A_B = cal(A,B,opt_array[0]); 
         B_C = cal(B,C,opt_array[1]); 
         C_D = cal(C,D,opt_array[2]); 
         rst[0] = cal(A_B,C_D,opt_array[1]); 
         rst[1] = cal(cal(A_B,C,opt_array[1]),D,opt_array[2]); 
         rst[2] =cal(cal(A,B_C,opt_array[0]),D,opt_array[2]); 
         rst[3] =cal(A,cal(B_C,D,opt_array[2]),opt_array[0]); 
         rst[4] =cal(A,cal(B,C_D,opt_array[1]),opt_array[0]); 
         check_rst(array,opt_array,rst); 
         return; 
      } 
      for(i=0;i<OPT_NUM;i++) 
      { 
          opt_array[idx] = i; 
          cal_result(array,opt_array,idx+1);        
      } 
}

/*取得所有运算排列并计算结果*/ 
void getcardarray(int *p_array,int idx) 
{ 
    int j; 
    if(idx>=CARDS_NUM)  
    { 
        cal_result(p_array,opt_array,0); 
        return; 
    } 
    for(j=0;j<CARDS_NUM;j++) 
    { 
        if(used_array[j]==0)  //未被占用 
        { 
            used_array[j]=1; 
            p_array[idx] = (j+1); 
            getcardarray(p_array,idx+1); 
            used_array[j]=0; 
        } 
    } 
}

int main() 
{ 
    getcardarray(p_array,0); 
    return 0; 
}

运行结果如图

换一组数据，1,5,5,5

运行结果如下

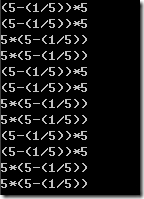
由于存在重复的数字，其实以上的排列只有4个,并且以上输出结果其实都是重复的，那么如何规避这些重复的结果呢，涉及到归一化的过程，后面还会再提到。值得注意的是，由于除法运算中的损失，结果未必为24.0，有些误差，在判断结果的时候，必须允许存在一定的误差才行

下一内容提示 五子棋

24点