NFA的确定化：这里指的 NFA 到 DFA的转换（不包括 ε 自动机），构造一个和 NFA 等价的 DFA。书中有介绍两种确定化的方法（子集法和造表法），这里只介绍造表法，造表法是比子集法简单而有效的一种确定化方法。

1，为什么不用子集法？？

           在子集法中，如果 NFA 的状态个数 n 比较大，那么，确定化后的 DFA 的状态个数 2^n-1 将更大，其中不少状态是不可达状态。

2，造表法算法的基本思想

           把 DFA 中的每一个状态对应 NFA中的一组状态。即由于 NFA 中的 t 是一个多值映射，所以在扫描到某个输入字符后可能达到的状态是集合，而造表法就是用 DFA 的状态记录该状态的集合。

3，造表法实现步骤

                      1，确定 DFA 的输入字母表（DFA 与 NFA 的输入字母表完全相同）；

                      2，再构建一张表，第一列记为状态子集 I ，对于字母表中的不同符号，在表中单设一列 Ia；

                      3，表中首行首列位置为 DFA 的开始状态；NFA 的开始状态为 q0，则以 [ q0 ] 作为 DFA 的开始状态，如有多个开始状态，即表示为 [ q0，q1，... q3 ]。多个状态加上“[]”括号即为一个子集元素（对应成 DFA 中的一个状态）；

                      4，根据首行首列的 I ，为字母表中每个输入字符 a 求其 Ia 并记入对应的 Ia 列中；如果此 Ia 不等同于第一列中已存在的所有状态子集 I，则将其顺序列入空行的第一列（Ia 的值为 状态子集 I 中每个元素经过 弧 a 所能到达后继状态的并集并用 “[]”形式表示）；

                      5，重复 4 步骤直至对每个 I 及 a 均已求得 Ia，并且无新的状态子集 Ia 加入第一列时为止；

                      6，重新命名第一列的每一个状态子集（只要第一列状态子集中包含有原 NFA 终止状态集合中元素的都是新 DFA 的终止状态），形成新的状态转换表，即为与 NFA 等价的 DFA；

4，for example：

                      NFA：

                      造表法确定化：

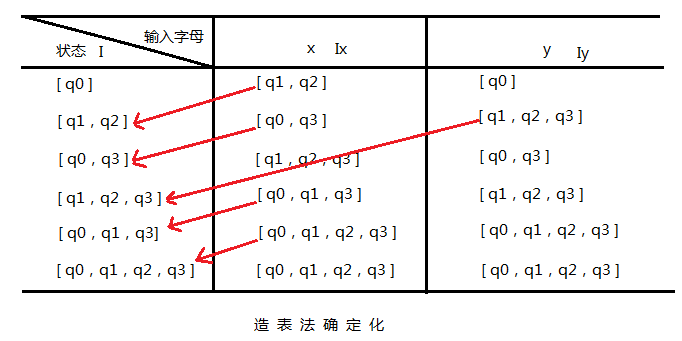
PS：每得到一个新状态，就继续求新状态对于 x，y 的映象，直到再没有新状态出现为止。

                      确定化后的状态转换表：

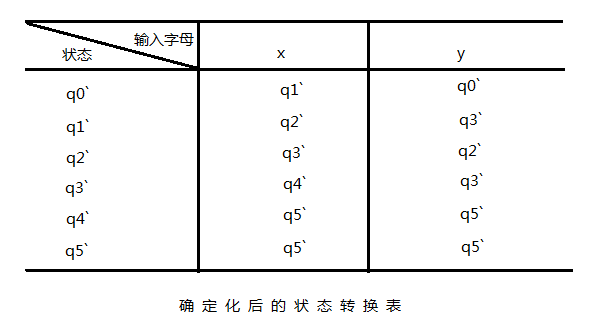
PS：[ q0 ]，[ q1，q2 ]，[ q0，q3 ]，[ q1，q2，q3 ]，[ q0，q1，q3 ]，[ q0，q1，q2，q3 ] 分别标记为 q0`，q1`，q2`，q3`，q4`，q5`。

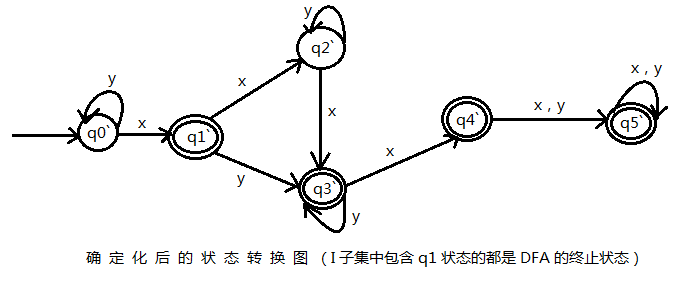
                      确定化后的 DFA 状态转换图：

本文出自 “珞辰的博客” 博客，谢绝转载！

NFA的确定化