In mathematics, Fibonacci numbers or Fibonacci series or Fibonacci sequence are the numbers of the following integer sequence:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...

By definition, the first two numbers in the Fibonacci sequence are 1 and 1, and each subsequent number is the sum of the previous two. In mathematical terms, the sequence F_n of Fibonacci numbers is defined by the recurrence relation F_n = F_{n - 1} + F_{n - 2} with seed values F₁ = 1 and F₂ = 1.

And your task is to find ΣF_i^K, the sum of the K-th power of the first N terms in the Fibonacci sequence. Because the answer can be very large, you should output the remainder of the answer divided by 1000000009.

Input

There are multiple test cases. The first line of input is an integer T indicates the number of test cases. For each test case:

There are two integers N and K (0 <= N <= 10¹⁸, 1 <= K <= 100000).

Output

For each test case, output the remainder of the answer divided by 1000000009.

Sample Input

5
10 1
4 20
20 2
9999 99
987654321987654321 98765

Sample Output

143
487832952
74049690
113297124
108672406

Hint

The first test case, 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 = 143.

The second test case, 1²⁰ + 1²⁰ + 2²⁰ + 3²⁰ =3487832979, and 3487832979 = 3 * 1000000009 + 487832952, so the output is 487832952.

题目大意

很明确，求菲波那契数列每个数的m次方的前n项和。

思路

当时看到m的取值范围就没敢在往下写，直到cf 255（446 C）有一道类似思路的线段树，官方的editorial里面给出了一个解释，就是求其二次剩余，然后该数列可以用幂差来表示。

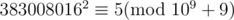
（二次剩余求解）

（以上三个式子均用拓展欧几里得推出，将sqrt5作为一个整体进行逆元求解）

（于是带入后我们就看到了一个剩余系的式子）

为什么要这么做的原因可能就和逆元的原理有些类似了，因为我们直到结果是整数，所以每一步都能在剩余系之中找到一个整数的运算代替了。

接下来就设

于是任意一个数的m次方为

对二项式展开之后其前n项求和

枚举k来求和即可

对于中间的一项等比数列的求和来加速，否则仍会超时。

求二次剩余以及各项系数值的code:（由于二次剩余大多有两个不同根，所以结果不同未必影响计算结果）

模板来自:blog.csdn.net/acdreamers/article/details/10182281

#include <cstdio>
#include <cstring>
#include <algorithm>
#define mod 1000000009
using namespace std;
long long sqrt5,s,r1,r2;
long long ts,w;
struct D{
    long long p,d;
};
void egcd(long long a,long long b,long long &x,long long &y)
{
    if (b==0)
    {
        x=1;
        y=0;
        return;
    }
    egcd(b,a%b,x,y);
    int t=x;
    x=y,y=t-a/b*y;
    return;
}
long long mypow(long long x,long long y,long long p)
{
    long long res=1,mul=x;
    while (y)
    {
        if (y & 1)
            res=res * mul % p;
        mul=mul * mul % p;
        y/=2;
    }
    return res;
}
D mul(D a,D b,long long m)
{
    D ans;
    ans.p=(a.p * b.p % m +a.d * b.d %m *w % m)%m;
    ans.d=(a.p * b.d % m +a.d * b.p% m)%m;
    return ans;
}
D power(D a,long long b,long long m)
{
    D ans;
    ans.p = 1;
    ans.d = 0;
    while (b)
    {
        if (b & 1)
        {
            ans=mul(ans,a,m);
        }
        b/=2;
        a=mul(a,a,m);
    }
    return ans;
}
long long sqre(long long x,long long y)
{
    if (y==2) return 1;
    if (mypow(x,(y-1)>>1,y)+1 == y)
        return -1;
    long long a,t;
    for (a=1;a<y;a++)
    {
        t= a * a - x;
        w= (t + y) % y;
        if (mypow(w,(y-1)>>1,y)+1 == y) break;
    }
    D tmp;
    tmp.p=a;
    tmp.d=1;
    D ans = power(tmp,(y+1)>>1,y);
    return ans.p;
}
int main()
{
    sqrt5=sqre(5,mod);
    printf("%I64d\n",sqrt5);
    long long x,y;
    egcd(5,mod,x,y);
    x=(x+mod)%mod;
    s=(sqrt5*x)%mod;
    printf("%I64d\n",s);

    egcd(2,mod,x,y);
    x=(x+mod)%mod;
    r1=((sqrt5+1)*x)%mod;
    r2=((-sqrt5+1+mod)*x)%mod;

    printf("%I64d\n",r1);
    printf("%I64d\n",r2);
    int T;
    return 0;
}

#include <cstdio>
#include <cstring>
#include <algorithm>
long long s=723398404,r1=308495997,r2=691504013;
long long mod=1000000009;
long long c[100005];
typedef long long Ma[2][2];
void egcd(long long a,long long b,long long &x,long long &y)
{
    if (b==0)
    {
        x=1;
        y=0;
        return;
    }
    egcd(b,a%b,x,y);
    int t=x;
    x=y,y=t-a/b*y;
    return;
}
long long mypow(long long x,long long y)
{
    long long res=1;
    while (y)
    {
        if (y%2)
            res=res * x % mod;
        x=x * x % mod;
        y/=2;
    }
    return res;
}
long long acce(long long x,long long y)//等比数列快速求和
{
    long long ans=0;
    long long powe=x;
    long long sum=x;
    long long mul=1;
    while (y)
    {
        if (y&1)
        {
            ans+=mul*sum;
            ans%=mod;
            mul*=powe;
            mul%=mod;
        }
        sum*=(powe+1);
        sum%=mod;
        powe*=powe;
        powe%=mod;
        y/=2;
    }
    return ans;
}
int main()
{
    int T;
    long long n,m;
    scanf("%d",&T);
    while (T--)
    {
        long long ans=0;
        scanf("%lld%lld",&n,&m);
        c[0]=1;
        long long x,y;
        for (long long i=1;i<=m;i++)
        {
            egcd(i,mod,x,y);
            x=(x+mod)%mod;
            c[i]=(c[i-1]*x)%mod;
            c[i]=(c[i]*(m-i+1))%mod;
        }
        for (long long i=0;i<=m;i++)
        {
            x=c[i];
            x=x * acce(mypow(d1,i)*mypow(d2,m-i)%mod,n)%mod;
            x=(x+mod)%mod;
            if ((m-i)%2)
            ans=(ans - x + mod)%mod;
            else
            ans=(ans + x + mod)%mod;
        }
        ans=ans*mypow(s,m)%mod;
        printf("%lld\n",ans);
    }
    system("pause");
    return 0;
}

[zoj 3774]Power of Fibonacci 数论(二次剩余 拓展欧几里得 等比数列求和)