实现子区域的快速求和，在人脸识别及相关算法中应用的Haar小波中很有用

原理：

计算一个简单矩形区域（（x1,y1）,(x2,y2)）中像素的和：

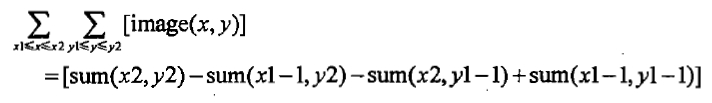
核心函数：

cvIntegral

程序：

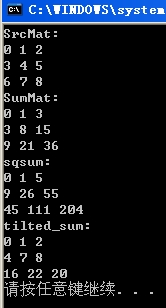
代码：

#include "cv.h"

#include "cxcore.h"

#include "highgui.h"

#include <iostream>

int integral(int argc,char** argv)

{

CvMat *src=http://www.mamicode.com/cvCreateMat(3,3,CV_32FC1);

float SrcData[9]={0,1,2,

              3,4,5,

  6,7,8

};

cvInitMatHeader(src,3,3,CV_32FC1,SrcData);

CvMat* sum=cvCreateMat(src->width+1,src->height+1,CV_64FC1);  //注意行列的大小为(W+1)*(H+1),如果原Mat的类型是uchar，这这里可以为32F，如果原Mat为32F，这里要用64F

CvMat* sqsum=cvCreateMat(src->width+1,src->height+1,CV_64FC1);

CvMat* tilted_sum=cvCreateMat(src->width+1,src->height+1,CV_64FC1);

cvIntegral(src,sum,sqsum,tilted_sum);

//打印原数组

std::cout<<"SrcMat:"<<std::endl;

for(int rows=0;rows<src->width;rows++)

{

float *pt=(float *)(src->data.ptr+rows*src->step);

for(int cols=0;cols<src->height;cols++)

{

float result=*(pt+cols);

std::cout<<result<<" ";

}

std::cout<<std::endl;

}

//打印积分结果，因为第一行第一列是为了计算效率而额外添加的，都为0，所以可以不打印

std::cout<<"SumMat:"<<std::endl;

for(int rows=1;rows<sum->width;rows++)

{

double *pt=(double *)(sum->data.ptr+rows*sum->step);

for(int cols=1;cols<sum->height;cols++)

{

double result=*(pt+cols);

std::cout<<result<<" ";

}

std::cout<<std::endl;

}

//打印sqsum，即sum的平方

std::cout<<"sqsum:"<<std::endl;

for(int rows=1;rows<sqsum->width;rows++)

{

double *pt=(double *)(sqsum->data.ptr+rows*sqsum->step);

for(int cols=1;cols<sqsum->height;cols++)

{

double result=*(pt+cols);

std::cout<<result<<" ";

}

std::cout<<std::endl;

}

//打印sqsum，即源图像平方的sum

std::cout<<"tilted_sum:"<<std::endl;

for(int rows=1;rows<tilted_sum->width;rows++)

{

double *pt=(double *)(tilted_sum->data.ptr+rows*tilted_sum->step);

for(int cols=1;cols<tilted_sum->height;cols++)

{

double result=*(pt+cols);

std::cout<<result<<" ";

}

std::cout<<std::endl;

}

return 0;

}

本文出自 “flyclc” 博客，请务必保留此出处http://flyclc.blog.51cto.com/1385758/1539805