首页 > 代码库 > 动态规划0—1背包问题
动态规划0—1背包问题
动态规划0-1背包问题
?
问题描写叙述:
给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为C。问应怎样选择装入背包的物品,使得装
入背包中物品的总价值最大?
?
对于一种物品,要么装入背包,要么不装。所以对于一种物品的装入状态能够取0和1.我们设物品i的装入状态为xi,xi∈ (0,1),此问题称为0-11背包问题。
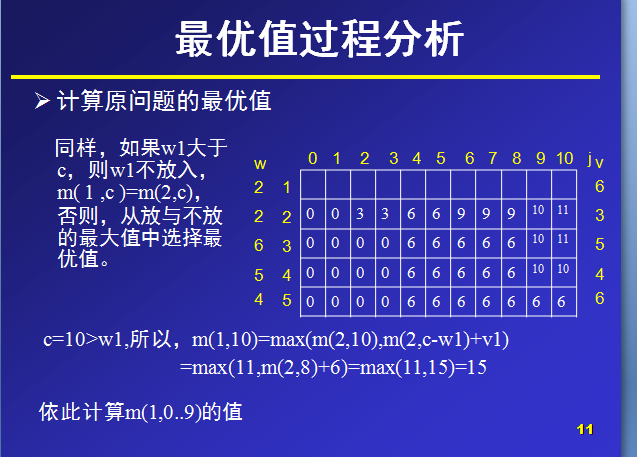
过程分析
数据:物品个数n=5,物品重量w[n]={0,2,2,6,5,4},物品价值V[n]={0,6,3,5,4,6},
(第0位,置为0,不參与计算,仅仅是便于与后面的下标进行统一,无特别用处,也可不这么处理。)总重量c=10.
?背包的最大容量为10,那么在设置数组m大小时,能够设行列值为6和11,那么,对于m(i,j)就表示可选物品为i…n背包容量为j(总重量)时背包中所放物品的最大价值。



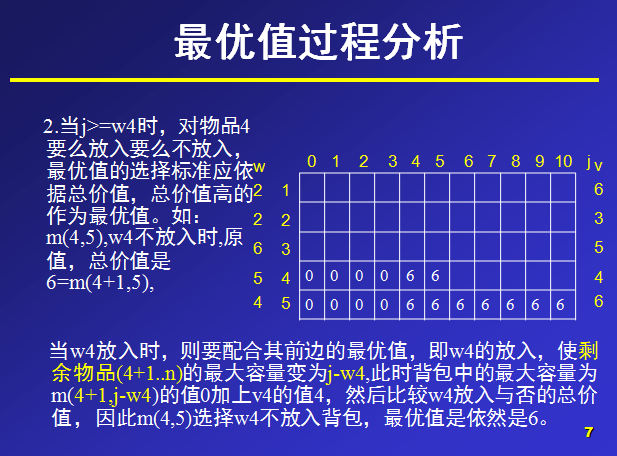
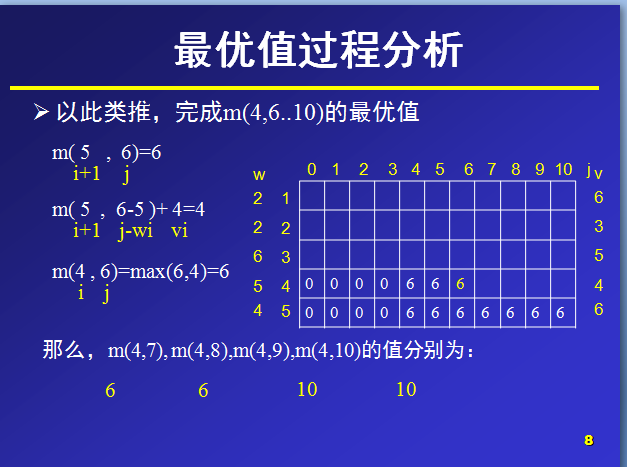
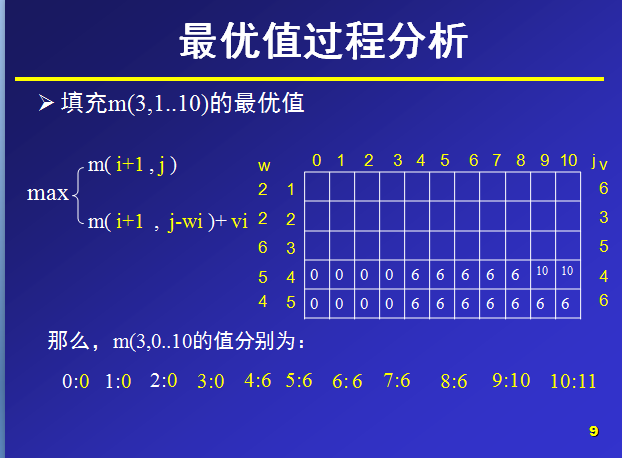
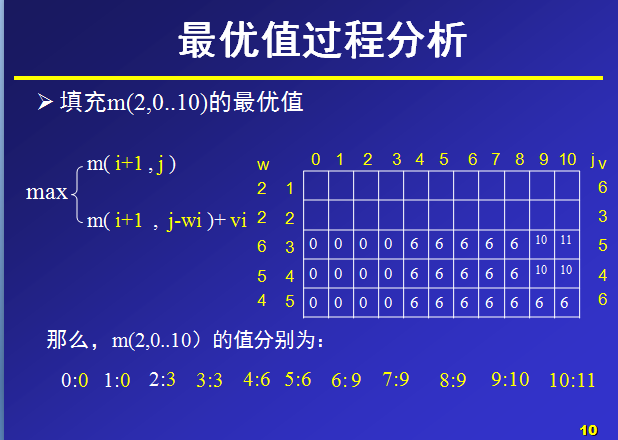







以下是自己写的源代码:
#include<stdio.h>#include<stdlib.h>#include<iostream>#include<queue>#include<climits>#include<cstring>using namespace std;const int c = 10; //背包的容量const int w[] = {0,2,2,6,5,4};//物品的重量,当中0号位置不使用 。 const int v[] = {0,6,3,5,4,6};//物品相应的待加,0号位置置为空。const int n = sizeof(w)/sizeof(w[0]) - 1 ; //n为物品的个数 int x[n+1];void package0_1(int m[][11],const int w[],const int v[],const int n)//n代表物品的个数 { //採用从底到顶的顺序来设置m[i][j]的值 //首先放w[n] for(int j = 0; j <= c; j++) if(j < w[n]) m[n][j] = 0; //j小于w[n],所相应的值设为0,否则就为能够放置 else m[n][j] = v[n]; //对剩下的n-1个物品进行放置。 int i; for(i = n-1; i >= 1; i--) for(int j = 0; j <= c; j++) if(j < w[i]) m[i][j] = m[i+1][j];//假设j < w[i]则,当前位置就不能放置,它等于上一个位置的值。 //否则,就比較究竟是放置之后的值大,还是不放置的值大,选择当中较大者。 else m[i][j] = m[i+1][j] > m[i+1][j-w[i]] + v[i]? m[i+1][j] : m[i+1][j-w[i]] + v[i]; }void answer(int m[][11],const int n){ int j = c; int i; for(i = 1; i <= n-1; i++) if(m[i][j] == m[i+1][j]) x[i] = 0; else { x[i] = 1; j = j - w[i]; } x[n] = m[i][j] ? 1 : 0; }int main(){ int m[6][11]={0}; package0_1(m,w,v,n); for(int i = 0; i <= 5; i++) { for(int j = 0; j <= 10; j++) printf("%2d ",m[i][j]); cout << endl; } answer(m,n); cout << "The best answer is:\n"; for(int i = 1; i <= 5; i++) cout << x[i] << " "; system("pause"); return 0;}
动态规划0—1背包问题
声明:以上内容来自用户投稿及互联网公开渠道收集整理发布,本网站不拥有所有权,未作人工编辑处理,也不承担相关法律责任,若内容有误或涉及侵权可进行投诉: 投诉/举报 工作人员会在5个工作日内联系你,一经查实,本站将立刻删除涉嫌侵权内容。
