首页 > 代码库 > AVL树

AVL树

2024-07-03 03:34:20   225人阅读

一棵AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树。实际高度只比logN多以一点，和普通二叉查找树相比，平衡二叉搜索树一般而言搜寻时间可节省25%左右（STL源码剖析P203）。

只有那些从插入点到根节点的路径上的节点的平衡可能被改变，因为只有这些节点的子树可能发生变化。

把需要重新平衡的节点称为a（左右子树高度差大于1）。注意，确定这个节点很重要，否则无法确定是下列哪一种情况。
造成不平衡的4种插入情况：
  • 对a的左儿子的左子树进行一次插入：右单转，旋转主体是失衡节点和左孩子以及它们的连线。
  • 对a的右儿子的右子树进行一次插入：左单转，旋转主体是失衡节点和右孩子以及它们的连线。
  • 对a的左儿子的右子树进行一次插入：左-右双旋转，先在失衡节点的儿子和孙子之间旋转而后再在失衡节点和它的新儿子之间旋转。
  • 对a的右儿子的左子树进行一次插入：右-左双旋转，先在失衡节点的儿子和孙子之间旋转而后再在失衡节点和它的新儿子之间旋转。

来一张维基百科的图，图中有一个错误，后两种情况的Root因该标在树的根上：


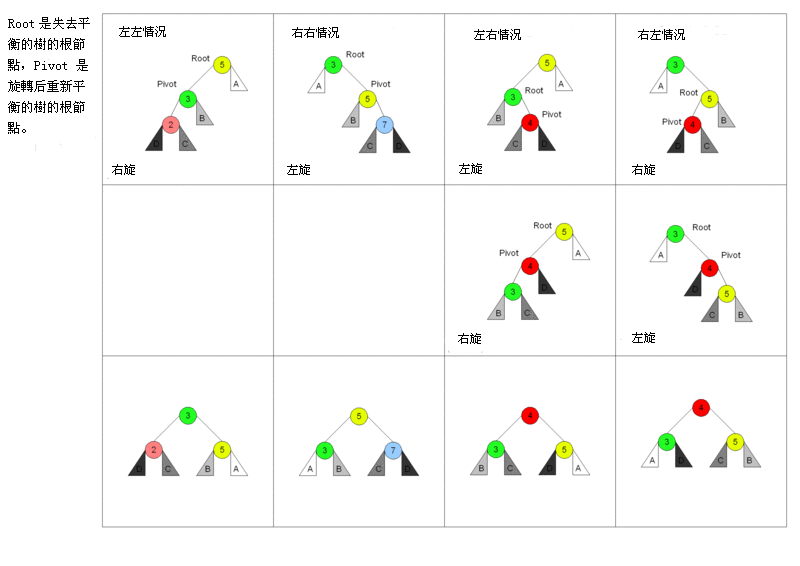
《算法设计与分析基础》中的一句话：
如果有若干个节点的平衡因子大于1，先找出最靠近新插入的叶子的不平衡节点，然后再旋转以该节点为根的树。

在程序设计中，和二叉查找树一样，通常使用递归地方法实现AVL树。
部分代码如下：
#include <stdio.h>
 
typedef int ElementType;
typedef struct AvlNode *Position;
typedef struct AvlNode *AvlTree;
 
struct AvlNode {
    ElementType Element;
    AvlTree Left;
    AvlTree Right;
    int Height;
};
 
int Max(int x, int y)
{
    return x > y ? x : y;
}
 
// 获得节点高度
int Height(Position p)
{
    if (p == NULL)
        return -1;
    else
        return p->Height;
}
 
// T跟左儿子进行右旋转
Position RightSingleRotate(Position T)
{
    Position NewRoot;
 
    NewRoot = T->Left;
    T->Left = NewRoot->Right;
    NewRoot->Right = T;
 
    // 修改高度
    T->Height = Max(Height(T->Left), Height(T->Right)) + 1;
    NewRoot->Height = Max(Height(NewRoot->Left), T->Height) + 1;
 
    return NewRoot;
}
 
// T跟右儿子进行左旋转
Position LeftSingleRotate(Position T)
{
    Position NewRoot;
 
    NewRoot = T->Right;
    T->Right = NewRoot->Left;
    NewRoot->Left = T;
 
    // 修改高度
    T->Height = Max(Height(T->Left), Height(T->Right)) + 1;
    NewRoot->Height = Max(Height(NewRoot->Right), T->Height) + 1;
 
    return NewRoot;
}
 
Position DoubleRotateWithLeft(Position T)
{
    // 先左旋转
    T->Left = LeftSingleRotate(T->Left);
    // 再右旋转
    return RightSingleRotate(T);
}
 
Position DoubleRotateWithRight(Position T)
{
    // 先右旋转
    T->Right = RightSingleRotate(T->Right);
    // 再左旋转
    return LeftSingleRotate(T);
}
 
AvlTree Insert(AvlTree T, ElementType x)
{
    if (T == NULL)
    {
        T = malloc(sizeof(struct AvlNode));
        if (T == NULL)
            return -1;
 
        T->Element = x;
        T->Left = T->Right = NULL;
        T->Height = 0;
    }
    else if (x < T->Element)
    {
        T->Left = Insert(T->Left, x);
        if (Height(T->Left) - Height(T->Right) == 2)
            if (x < T->Left->Element)
                T = RightSingleRotate(T);       // 左-左：右单旋转
            else
                T = DoubleRotateWithLeft(T);    // 左-右：左右双旋转
 
    }
    else if (x > T->Element)
    {
        T->Right = Insert(T->Right, x);
        if (Height(T->Right) - Height(T->Left) == 2)
            if (x > T->Right->Element)
                T = LeftSingleRotate(T);        // 右-右：左单旋转
            else
                T = DoubleRotateWithRight(T);   // 右-左：右左双旋转
    }
 
    T->Height = Max(Height(T->Left), Height(T->Right)) + 1; // 调整高度
    return T;
}
 
void MiddleTraversal(AvlTree T)
{
    if (T == NULL)
        return;
 
    MiddleTraversal(T->Left);
    printf("%d ", T->Element);
    MiddleTraversal(T->Right);
}
 
int main()
{
    AvlTree tree = NULL;
    int i;
 
    for (i = 1; i <= 16; i++)
        tree = Insert(tree, i);
 
    MiddleTraversal(tree);
 
    return 0;
}



参考：
《数据结构于算法分析》 P80.
《STL源码剖析》 P203.


联系
我们