如何使用随机性矩阵乘法，随机算法在验证多项式的恒等问题比确定算法要快，而且在准确性上面也是可以接受的。假设有A，B，C三个n*n的矩阵。为了方便起见假定对模2的整数计算。我们想要快速的验证AB=C。首先想到的方法就是通过矩阵计算AB得到的矩阵与矩阵C对比。但是简单的矩阵乘法的时间复杂度为O(n^3),就算是经过优化的矩阵乘法算法的时间复杂度为O(n^2.37)。显然这样的时间复杂度不为我们所接受。

     我们可以再次使用随机算法来在一个可以接受的出错概率下来验证。算法首先抽取一个向量r=(r1,r2,......rn)^T∈{0,1}^n,然后计算A（Br）的值，也计算C r的值。如果A（B r）≠（C r）的值则AB≠C，否则AB=C。计算一个矩阵--向量的乘法，时间复杂度为O(n^2).下面将介绍AB≠C时但是却反回AB=C的概率的上界。

如果AB≠C，且r是均匀随机的从{0,1}^n获取数据，则有Prob（A（B r）=（C r））≤1/2。

给出上述的证明如下：r=(r1,r2,......rn)^T是均匀随机的从{0,1}^n获取数据等价于从{0,1}中独立随机的选取每一个ri。如果每一个ri都是随即独立的从{0,1}中选取，在整个样本空间会有2^n中可能，那么选择其中的一个r=(r1,r2,......rn)^T的概率为1/(2^n)的可能性，即为如果向量r全为1这种可能性为1/(2^n)。

设D═AB—C≠0，那么A（B r）≠（C r）意味着（D r）=0，显然D不是全零矩阵，可以得出必有一个非零元素设为d11。那么根据矩阵的乘法计算法则有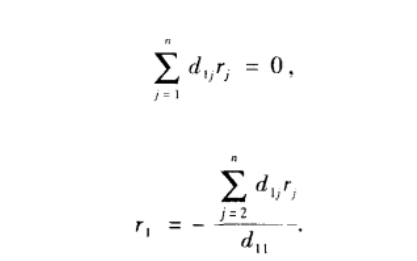

现在介绍一种思想，首先不考虑向量r，假定我们是从rn到r1依次从{0,1}中独立且均匀的随机选取ri，现在仅考虑r1的情况，假设r2,......rn都已经固定所以是等式成立的条件仅仅取决于r1的值，是等式成立的r1之多只有一种选择，r1的取值为{0,1}，所以Prob（A（B r）=（C r））≤1/2。这种思想称之为延迟决策原理，当存在多个随机变量的时候则在算法中先固定一部分，其余的看作是随机变量，然后来分析。

     为了改善Prob（A（B r）=（C r））≤1/2这样的犯错概率，我们利用算法具有单边错误的性质并且多次运行算法，如果找到某个r使得A（B r）≠（C r）成立则算法将正确的返回AB≠C。如果总发现A（B r）=（C r），则算法返回AB═C，但是会存在一定的犯错概率，这个一次执行这个错误概率≤1/2，当我们独立重复K次时，犯错的概率将会降到≤1/（2^k）

验证矩阵乘法