希尔伯特变换的物理意义十分简单：把信号的所有频率分量的相位推迟90度。
也就是说，如果原信号可以表示成，
则经过希尔伯特变换后的信号为。
这一点通过希尔伯特变换的频域形式很容易看出来：
，其中

当然，我知道题主最感兴趣的是：把相位推迟90度有什么用？
答案是：希尔伯特变换可以用来做解调器，调幅、调频都能解。

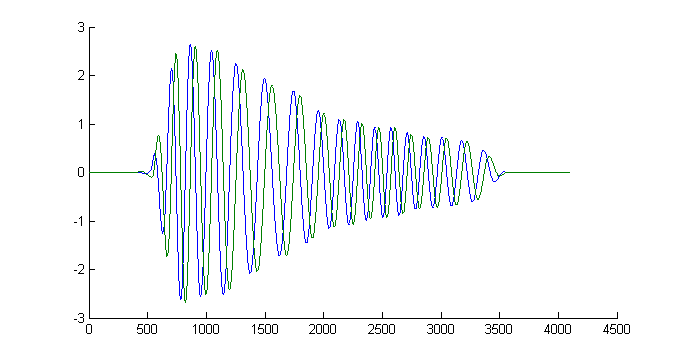
如图，蓝色是一个调制信号，其幅度、频率都经过了调制。
绿色是蓝色信号的希尔伯特变换。由于调制波的幅度和瞬时频率变化都很慢（与载波频率相比），其频率成分比较单一（都集中在载波频率附近），所以希尔伯特变换的效果——相位推迟90度——是很明显的。
现在构造信号，我们想办法把这个信号在三维空间中画出来。
下面这张图中有三个轴：时间轴、实轴、虚轴。
时间轴和实轴构成的平面上画出了（蓝色），
时间轴和虚轴构成的平面上画出了（绿色），
三维空间中画出了（红色）。
可以看出，的样子就像一根粗细、疏密都在变化的弹簧。
在任意一个时刻，我们都可以读出的瞬时幅度和瞬时相位：
瞬时幅度为，瞬时相位的正切值为。
而瞬时相位对时间的导数就是瞬时频率。

这样，我们就利用希尔伯特变换从一个幅度、频率均被调制的调制波中把幅度、频率都解调了出来。

当然，实际的解调器中并不是这么做的，一个重要的原因就是希尔伯特变换不是因果的，不能实时解调。