平衡二叉树又称AVL树。它或者是颗空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。若将二叉树节点的平衡因子BF定义为该节点的左子树的深度减去它的右子树的深度，则平衡二叉树上全部节点的平衡因子仅仅可能为-1,0,1.仅仅要二叉树上有一个节点的平衡因子的绝对值大于1，那么这颗平衡二叉树就失去了平衡。

如果我们已经有棵平衡二叉树，如今让我们来看看插入节点后，原来节点失去平衡后，我们进行选择的处理方式。

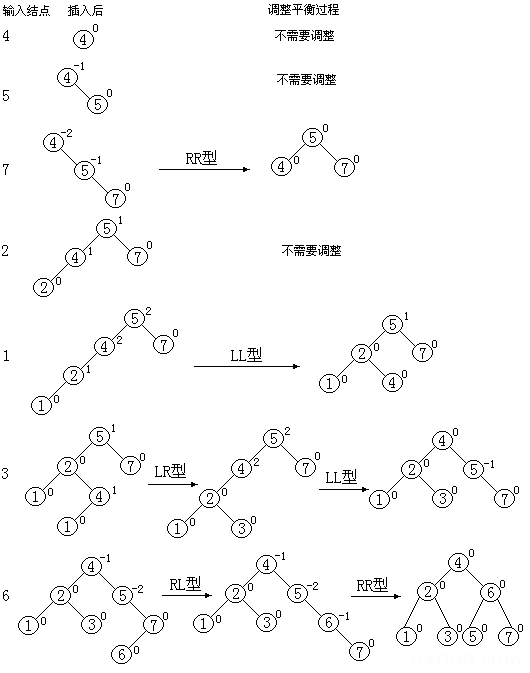
平衡二叉树多用于查找数据，所以平衡二叉树又是颗二叉排序树。

那么怎样创建一颗平衡二叉树呢？

创建平衡二叉树，我们採用依次插入节点的方式进行。而平衡二叉树上插入节点採用递归的方式进行。递归算法例如以下：

（1）      若该树为一空树，那么插入一个数据元素为e的新节点作为平衡二叉树的根节点，树的高度添加1。

（2）      若待插入的数据元素e和平衡二叉树（BBST）的根节点的keyword相等，那么就不须要进行插入操作。

（3）      若待插入的元素e比平衡二叉树（BBST）的根节点的keyword小，并且在BBST的左子树中也不存在和e有同样keyword的节点，则将e插入在BBST的左子树上，并且当插入之后的左子树深度添加1时，分别就下列情况处理之。

(a)    BBST的根节点的平衡因子为-1（右子树的深度大于左子树的深度）：则将根节点的平衡因子更改为0，BBST的深度不变；

(b)    BBST的根节点的平衡因子为0（左右子树的深度相等）：则将根节点的平衡因子改动为1，BBST的深度添加1；

(c)    BBST的根节点的平衡因子为1（左子树的深度大于右子树的深度）：若BBST的左子树根节点的平衡因子为1，则须要进行单向右旋转平衡处理，而且在右旋处理后，将根节点和其右子树根节点的平衡因子更改为0，树的深度不变；

若BBST的左子树根节点的平衡因子为-1，则需进行先向左，后向右的双向旋转平衡处理，而且在旋转处理之后，改动根节点和其左，右子树根节点的平衡因子，树的深度不变；

（4）      若e的keyword大于BBST的根节点的keyword，并且在BBST的右子树中不存在和e有同样keyword的节点，则将e插入到BBST的右子树上，并且当插入之后的右子树深度加1时，分别就不同的情况处理之。

（a）      BBST的根节点的平衡因子是1（左子树的深度大于右子树的深度）：则将根节点的平衡因子改动为0，BBST的深度不变；

（b）      BBST的根节点的平衡因子是0（左右子树的深度相等）：则将根节点的平衡因子改动为-1，树的深度加1；

（c）      BBST的根节点的平衡因子为-1（右子树的深度大于左子树的深度）：若BBST的右子树根节点的平衡因子为1，则须要进行两次选择，第一次先向右旋转，再向左旋转处理，而且在旋转处理之后，改动根节点和其左，右子树根节点的平衡因子，树的深度不变；

若BBST的右子树根节点的平衡因子为1，则须要进行一次向左的旋转处理，而且在左旋之后，更新根节点和其左，右子树根节点的平衡因子，树的深度不变；

以下附上本人的代码：

#include <stdio.h>
#include <stdlib.h>
/************************************************************************/
/*                    平衡二叉树---AVL                                  */
/************************************************************************/
#define LH +1
#define EH  0
#define RH -1
typedef int ElemType;
typedef struct BSTNode{
	ElemType data;
	int bf;//balance flag
	struct BSTNode *lchild,*rchild;
}*PBSTree;

void R_Rotate(PBSTree* p)
{
	PBSTree lc = (*p)->lchild;
	(*p)->lchild = lc->rchild;
	lc->rchild = *p;
	*p = lc;
}

void L_Rotate(PBSTree* p)
{
	PBSTree rc = (*p)->rchild;
	(*p)->rchild = rc->lchild;
	rc->lchild = *p;
	*p = rc;
}

void LeftBalance(PBSTree* T)
{
	PBSTree lc,rd;
	lc = (*T)->lchild;
	switch (lc->bf)
	{
	case LH:
		(*T)->bf = lc->bf = EH;
		R_Rotate(T);
		break;
	case RH:
		rd = lc->rchild;
		switch(rd->bf)
		{
		case LH:
			(*T)->bf = RH;
			lc->bf = EH;
			break;
		case EH:
			(*T)->bf = lc->bf = EH;
			break;
		case RH:
			(*T)->bf = EH;
			lc->bf = LH;
			break;
		}
		rd->bf = EH;
		L_Rotate(&(*T)->lchild);
		R_Rotate(T);
		break;
	}
}

void RightBalance(PBSTree* T)
{
	PBSTree lc,rd;
	lc= (*T)->rchild;
	switch (lc->bf)
	{
	case RH:
		(*T)->bf = lc->bf = EH;
		L_Rotate(T);
		break;
	case LH:
		rd = lc->lchild;
		switch(rd->bf)
		{
		case LH:
			(*T)->bf = EH;
			lc->bf = RH;
			break;
		case EH:
			(*T)->bf = lc->bf = EH;
			break;
		case RH:
			(*T)->bf = EH;
			lc->bf = LH;
			break;
		}
		rd->bf = EH;
		R_Rotate(&(*T)->rchild);
		L_Rotate(T);
		break;
	}
}

int InsertAVL(PBSTree* T,ElemType e,bool* taller)
{
	if ((*T)==NULL)
	{
		(*T)=(PBSTree)malloc(sizeof(BSTNode));
		(*T)->bf = EH;
		(*T)->data = http://www.mamicode.com/e;>