首页 > 代码库 > 【机器学习算法-python实现】协同过滤（cf）的三种方法实现

【机器学习算法-python实现】协同过滤（cf）的三种方法实现

2024-07-04 21:57:22   228人阅读

(转载请注明出处：http://blog.csdn.net/buptgshengod)

1.背景

      协同过滤（collaborative filtering）是推荐系统常用的一种方法。cf的主要思想就是找出物品相似度高的归为一类进行推荐。cf又分为icf和ucf。icf指的是item collaborative filtering，是将商品进行分析推荐。同理ucf的u指的是user，他是找出知趣相似的人，进行推荐。通常来讲icf的准确率可能会高一些，通过这次参加天猫大数据比赛，我觉得只有在数据量非常庞大的时候才适合用cf，如果数据量很小，cf的准确率会非常可怜。博主在比赛s1阶段，大概只有几万条数据的时候，尝试了icf，准确率不到百分之一。。。。。

2.常用方法

     cf的常用方法有三种，分别是欧式距离法、皮尔逊相关系数法、余弦相似度法。
       测试矩阵,行表示三名用户，列表示三个品牌，对品牌的喜爱度按照1~5增加。


（1）欧氏距离法

        就是计算每两个点的距离，比如Nike和Sony的相似度。数值越小，表示相似的越高。
def OsDistance(vector1, vector2):
    sqDiffVector = vector1-vector2
    sqDiffVector=sqDiffVector**2
    sqDistances = sqDiffVector.sum()
    distance = sqDistances**0.5
    return distance


（2）皮尔逊相关系数 

       

        两个变量之间的相关系数越高，从一个变量去预测另一个变量的精确度就越高，这是因为相关系数越高，就意味着这两个变量的共变部分越多，所以从其中一个变量的变化就可越多地获知另一个变量的变化。如果两个变量之间的相关系数为1或-1，那么你完全可由变量X去获知变量Y的值。

·         当相关系数为0时，X和Y两变量无关系。

·         当X的值增大，Y也增大，正相关关系，相关系数在0.00与1.00之间

·         当X的值减小，Y也减小，正相关关系，相关系数在0.00与1.00之间

·         当X的值增大，Y减小，负相关关系，相关系数在-1.00与0.00之间

          当X的值减小，Y增大，负相关关系，相关系数在-1.00与0.00之间

相关系数的绝对值越大，相关性越强，相关系数越接近于1和-1，相关度越强，相关系数越接近于0，相关度越弱。

clip_image003

           

            在python中用函数corrcoef实现，具体方法见http://infosec.pku.edu.cn/~dulz/doc/Numpy_Example_List.htm


（3）余弦相似度

         通过测量两个向量内积空间的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1，而其他任何角度的

余弦值都不大于1;并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两

个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相

反的方向时，余弦相似度的值为-1。在比较过程中，向量的规模大小不予考虑，仅仅考虑到向量的指向方向。余弦相

似度通常用于两个向量的夹角小于90°之内，因此余弦相似度的值为0到1之间。

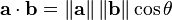
       \mathbf{a}\cdot\mathbf{b}=\left\|\mathbf{a}\right\|\left\|\mathbf{b}\right\|\cos\theta
       
def cosSim(inA,inB):
    num = float(inA.T*inB)
    denom = la.norm(inA)*la.norm(inB)
    return 0.5+0.5*(num/denom)


联系
我们