设（x1, y1), (x2,y2), ...(xk,yk)为输入样本，注意这里的xi本身是一个向量。

假设拟合多项式为：

则通过使用下面的最小平方差拟合方法：

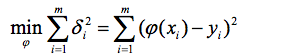
可得：

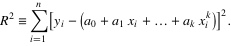
拟合过程变成求上式的最小值，相信学过高数的童鞋应该都知道怎么求，对的以此对系数a0,a1....求偏导数，使其为零，最后可得K+1组方程：

.......................

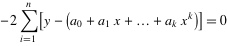
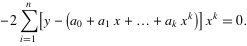
移项，表示成矩阵为：

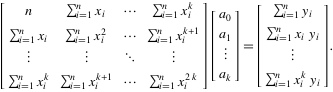
对范德蒙矩阵进行化简的到：

即XA=Y，所以系数向量 A=（X‘X)-1X’Y,其中X‘表示转置，-1是求逆矩阵，这便是斯坦福大学里机器学习第二节课的中梯度递减算法的推导公式。

实际编程，只需求出系数向量，便可以进行后续的预测了！！！！

最小二乘法完成曲线拟合公式