回归问题是根据一组特征(feature)，预测一个值，和分类问题不同，这个值是连续的，分类问题的预测值是离散的。

m：训练集的记录条数

x：训练集中的一条记录的输入变量部分，或者说特征值

y：训练集中的记录的输出变量，或者说目标值

假设特征的个数是1，即有一组(x, y)的值，针对新的x的值，预测y的值。模型如下：

问题转化为求θ0和θ1的值。

最小二乘法，得出cost function：

问题转化为求上面②式的最小值。

最小值求解问题有多种解法，下面介绍梯度下降法和normal equation法。

梯度下降法：

从一组θ0和θ1的值开始，每次迭代都改变θ0和θ1的值，使得②式的值越来越小，直到收敛。

上式中，α称为learning rate，这个值既不能太大也不能太小(需要在实际操作时，没迭代n次，记下J(θ0, θ1)的值，观察J(θ0, θ1)是否越来越小)，如果太大，J(θ0, θ1)可能无法收敛，如果太小，要迭代的次数太多，运行时间会很长。

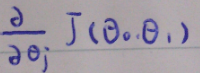
上图表示J(θ0, θ1)对θj的偏导数。

同时改变θ0和θ1的值，θ0 := θ0 - α(J(θ0, θ1)对θ0的偏导数)，θ1 := θ1 - α(J(θ0, θ1)对θ1的偏导数)，直到J(θ0, θ1)的值收敛(例如，两次迭代，J(θ0, θ1)的值减小的程度小于0.001)。

normal equation：

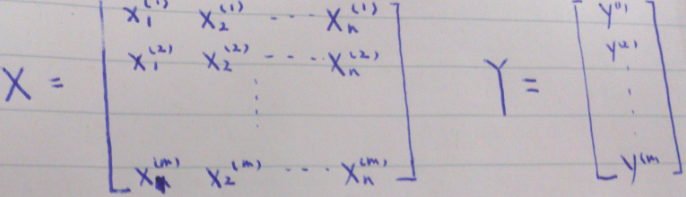
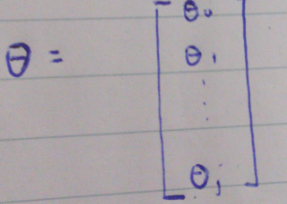
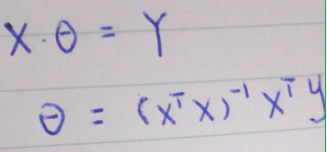
两种方法的比较：

梯度下降 vs normal equation
梯度下降需要选定一个α，normal equation不需要
梯度下降需要迭代很多次，normal equation不需要
梯度下降需要考虑scale问题，normal equation不需要

梯度下降在特征数目很大的时候，works well，normal equation在矩阵计算时会很expensive，(特征数大概10000左右时可以考虑用梯度下降)

还有一些其他更复杂的方法：

conjugate gradient(共轭梯度法)
BFGS(拟牛顿法)
L-BFGS

等

在实际使用梯度下降时，有几个技巧

1. 把特征值尽量归化到同一区间(在使用spark mllib的训练数据时发现训练集的数据大多是0到1区间的double值，可能是这个原因)

2. 根据实际操作情况调整learning rate的值。

线性回归